Aufgabenstellung:
Betrachtet wird das folgende System, dessen nichtlinearer Teil durch ein Kennlinienfeld beschrieben wird:
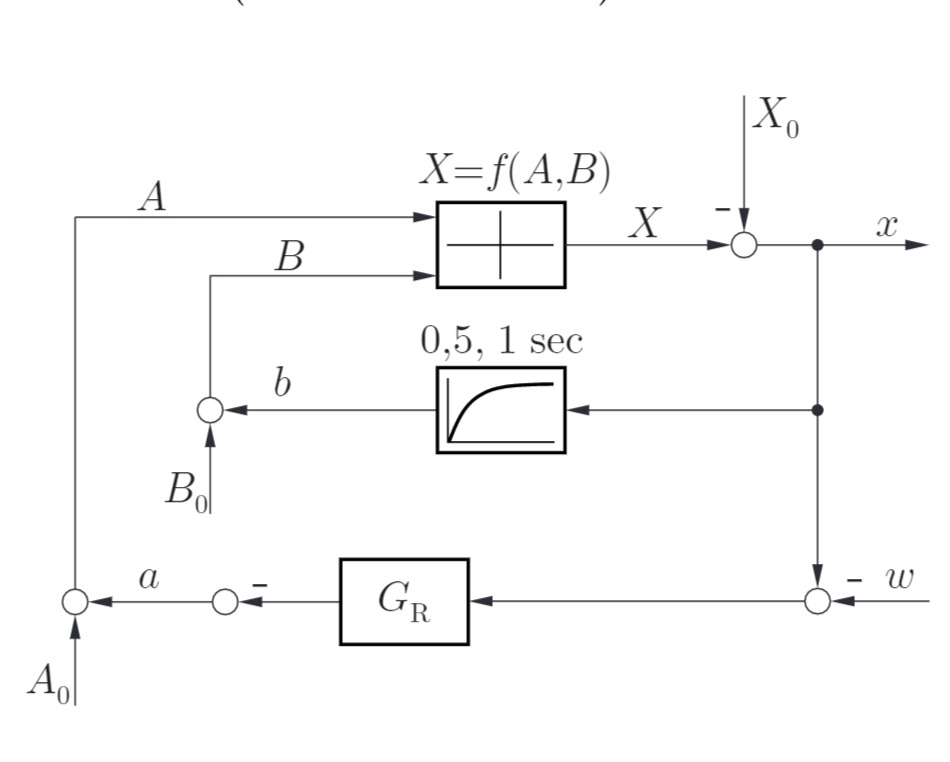
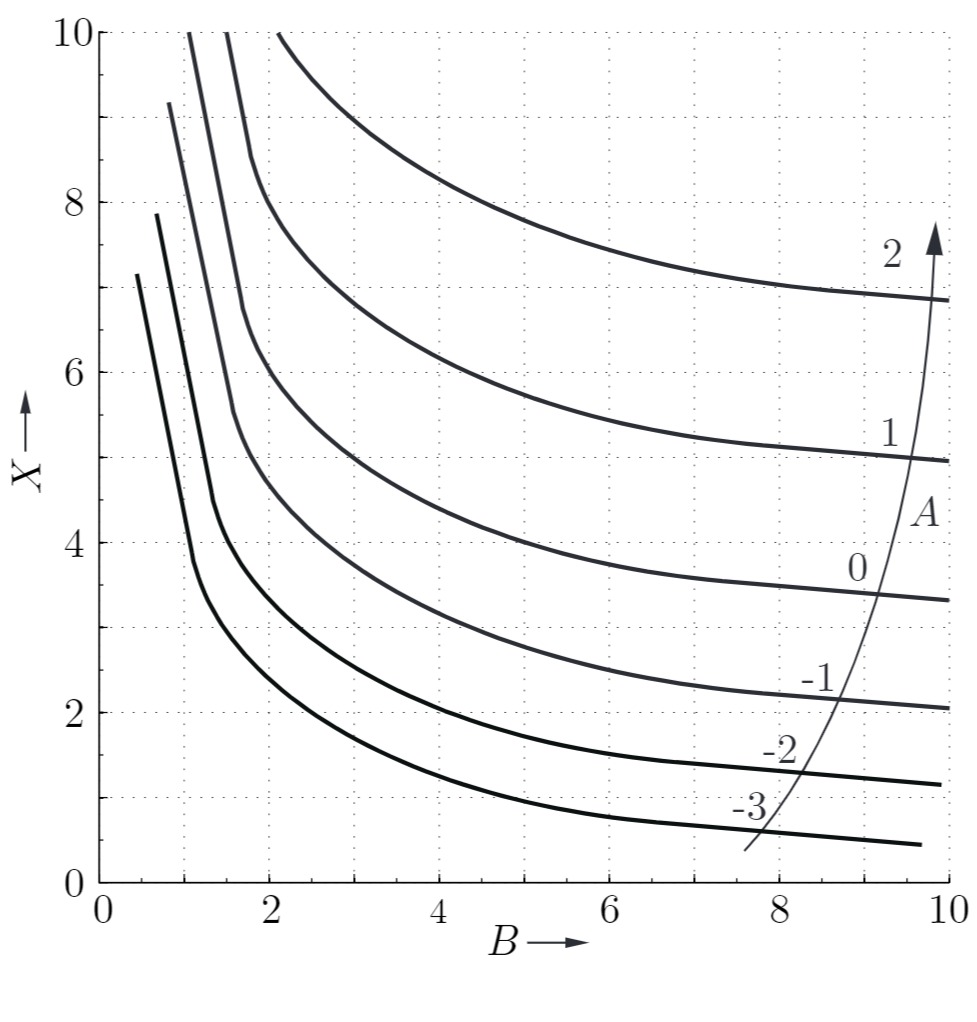
Es gilt zunächst:
a) Bestimmen Sie
b) Das stabile System erfährt nun die Anregung
Nun soll das System mit einem
c) Ermitteln Sie die statischen Endwerte von
Hinweis: Die folgende Teilaufgabe kann unabhängig gelöst werden.
d) Bestimmen Sie die Linearisierung
Lösungsweg:
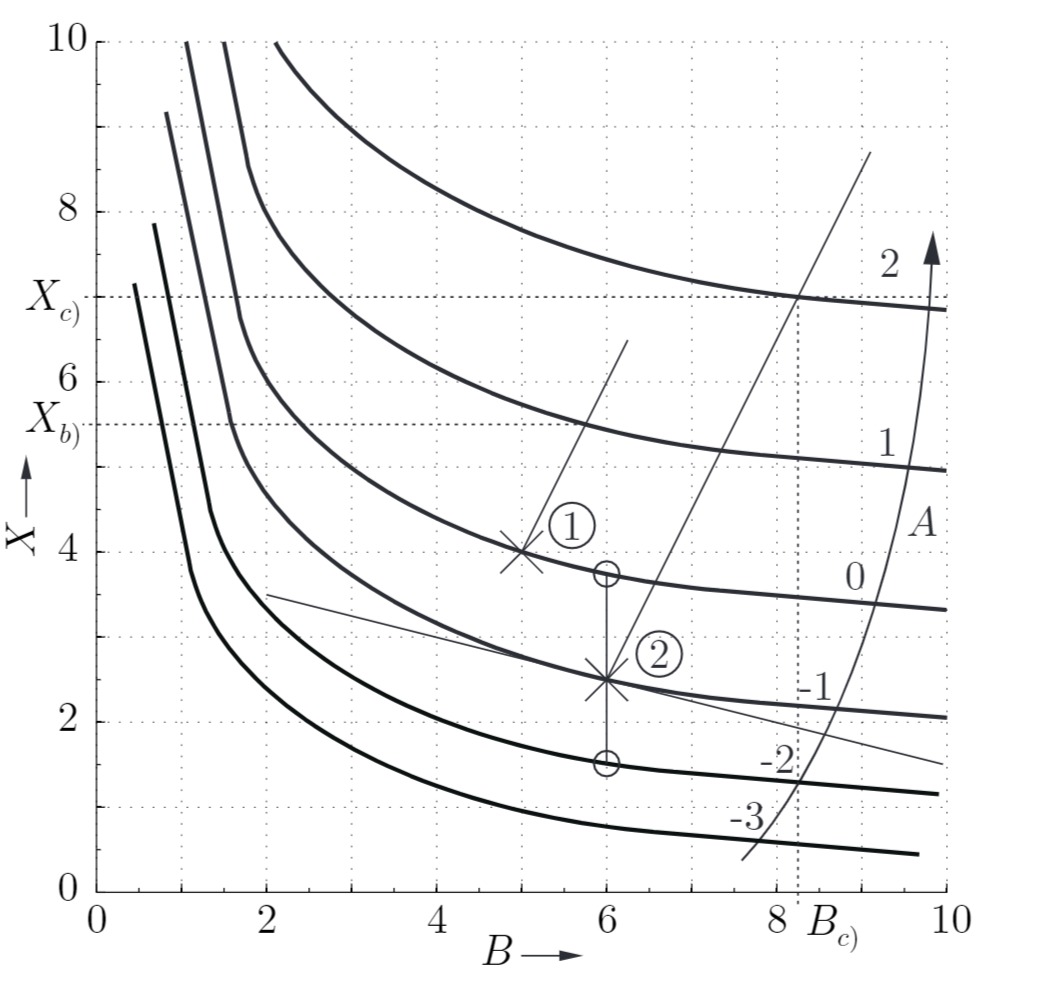
Hinweis: Das Kennlinienfeld mit eingezeichneten Werten wird nach Aufgabe d) aufgedeckt
a)
Ablesen im Kennfeld im Arbeitspunkt (1) ergibt
b) statischer Endwert von
Im statischen Zustand
Ausgehend vom Arbeitspunkt kann dieser Zusammenhang als Gerade in das Kennfeld eingetragen werden, um den Schnittpunkt mit
Dort kann der neue statische Endwert von
c) statischen Endwerte von
Der integrierende Regler verhindert eine bleibende Regelabweichung, sodass gilt:
Im Kennlinienfeld kann nun der Schnittpunkt zwischen der Horizontalen
Ablesen von
d) Linearisierung
Die Werte für
Diagramm zu den Aufgaben a) - d):