3 / 5

Aufgabenstellung:

Gegeben ist folgender kaskadierter Regelkreis:

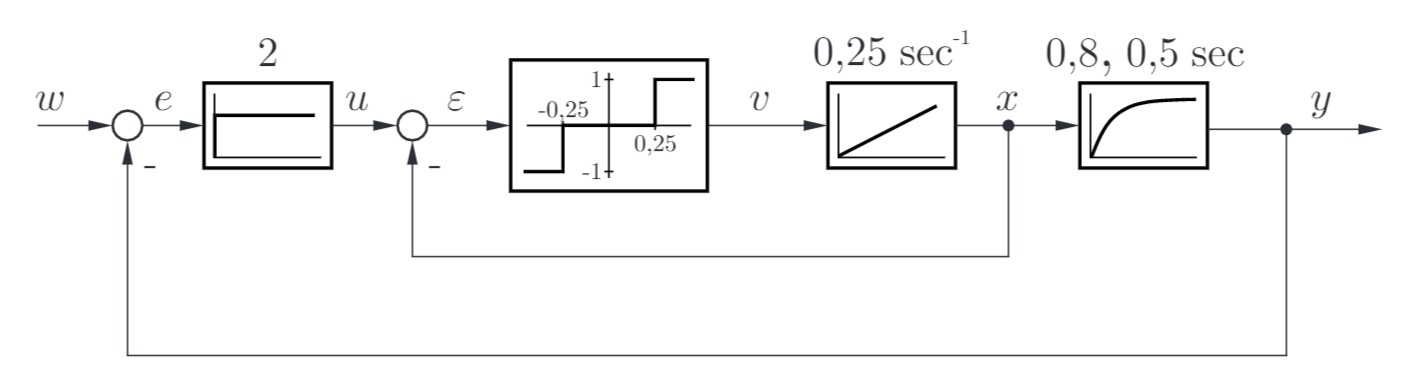
Abbildung

mit und

a) Bestimmen Sie . 
b) Bestimmen Sie die Übertragungsfunktion

c) Berechnen Sie den Umschaltzeitpunkt. Für ist die Betrachtung der Asymptoten ausreichend. 
d) Zeichnen Sie die realen Verläufe von und in die beigefügten Diagramme. 

Lösungsweg:

Drücke auf "Aufdecken" um dir den ersten Schritt der Lösung anzuzeigen

a)

b)

Das Übertragungsverhalten entspricht einem -Glied

c)

Zeitverläufe für :

Der Umschaltzeitpunkt ist der Zeitpunkt, an dem die obere Schaltschwelle unterschritten wird, er lässt sich also über die Bedingung bestimmen:

Hinweis: Da , gilt . Somit entspricht bis zum Umschaltzeitpunkt der Sprungantwort eines -Glieds, dessen Asymptote eine Rampe mit der Steigung und einer Totzeit von ist. entspricht anfangs hingegen der Sprungantwort des Integrators, also einer idealen Rampe.

d) Diagramme:

Abbildung

Abbildung

Hinweis:

Am Umschaltzeitpunkt springt der Integratoreingang auf , weshalb der Integratorausgang ab dann konstant bleibt: . Aufgrund der Trägheit des nachgeschalteten bleibt nach dem Umschaltzeitpunkt hingegen nicht konstant , sondern steigt noch weiter. Der stationäre Endwert ergibt sich mit Hilfe des Grenzwertsatzes zu

Da für konstantes und auch konstant bleibt, liegt man ab dem Umschaltzeitpunkt dauerhaft zwischen beiden Schaltschwellen des Dreipunkt-Glieds und es kommt zu keinem weiteren Schaltvorgang.

Lösung:

  4. siehe Musterlösung