Aufgabenstellung:
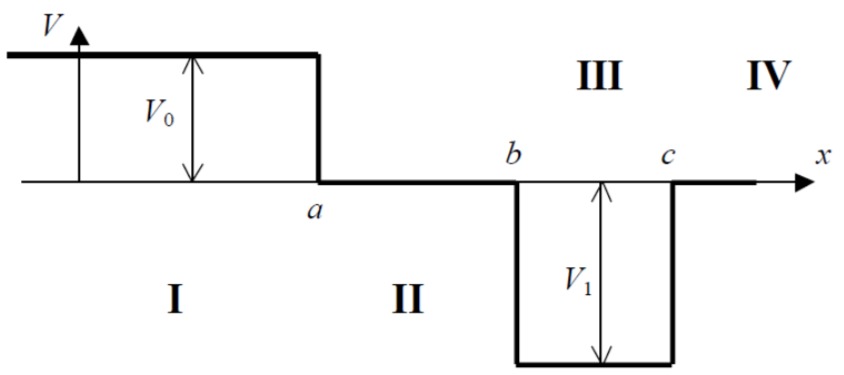
Betrachten Sie die abgebildete stückweise konstante Potentiallandschaft in der Abbildung. Ein von rechts einlaufendes Teilchen habe die Masse
- Geben Sie die Ansätze für die Wellenfunktionen für die verschiedenen Regionen I-IV an und verwenden Sie dabei
und . Die Schrödingergleichung muss nicht gelöst werden. - Stellen Sie die Anschlussbedingung für
auf. - Unter der Annahme, dass in Bereich III gebundene Zustände existieren, stellen Sie wie in Aufgabe a) die Lösungen für die vier Regionen auf.
Lösungsweg:
Drücke auf "Aufdecken" um dir den ersten Schritt der Lösung anzuzeigen
a) Ansätze für die Wellenfunktionen
Für die verschiedenen Regionen lassen sich folgende Ansätze aufstellen:
b) Anschlussbedingung für die Stelle
Stetigkeit von
c) Lösungen
Wenn gebundene Zustände in Region III existieren, muss die Energie des Teilchens
Lösung:
Siehe Lösungsweg.