Aufgabenstellung:
Bei einem Streuexperiment tritt Compton-Streuung auf. Unter dem Streuwinkel
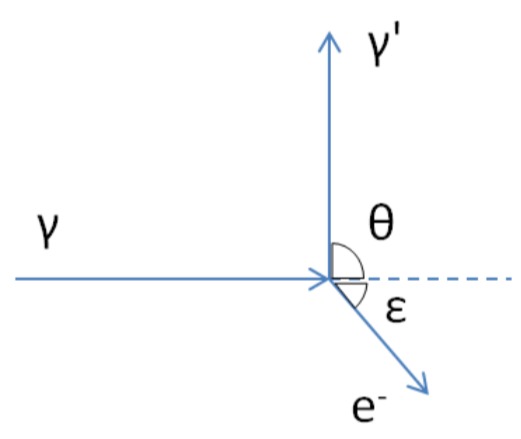
- Bestimmen Sie die Frequenz der einfallenden Strahlung.
- Berechnen Sie die Geschwindigkeit des gestoßenen Elektrons.
- Berechnen Sie den Winkel
, den die Flugrichtung des gestoßenen Elektrons mit der Richtung der Primärstrahlung einschließt.
Lösungsweg:
a) Frequenz der einfallenden Strahlung
Es gilt für den Compton-Effekt:
mit der Comptonwellenlänge
Man erhält für die Wellenlänge der einfallenden Strahlung
Und somit als Frequenz:
b) Geschwindigkeit des gestoßenen Elektrons
Die übertragene Energie auf das Elektron ist
Aus der Energie-Impuls Beziehung erhält man eine Formel für den Impuls
und aus der Definition des relativistischen Impulses erhält man eine Gleichung für dessen Geschwindigkeit
c) Winkel
Da der Streuwinkel der Strahlung
erhält man ein rechtwinkliges Dreieck und es gilt: