Aufgabenstellung:
-
In einem Versuch werden Hüllenelektronen mit Röntgenstrahlung beschossen. Ab welcher Wellenlänge der Photonen kann man die Elektronen als frei betrachten?
Mit dem folgenden Versuchsaufbau werden Messungen durchgeführt. Hierbei werden zunächst in einer Röntgenröhre-Quanten erzeugt. Durch Blenden und einen Filter gelangen nur Quanten mit einer speziellen Richtung und Frequenz im Streukörper an. Nachdem die Quanten gestreut wurden, wird mit Hilfe von Bragg-Reflexion ihre neue Frequenz bestimmt. 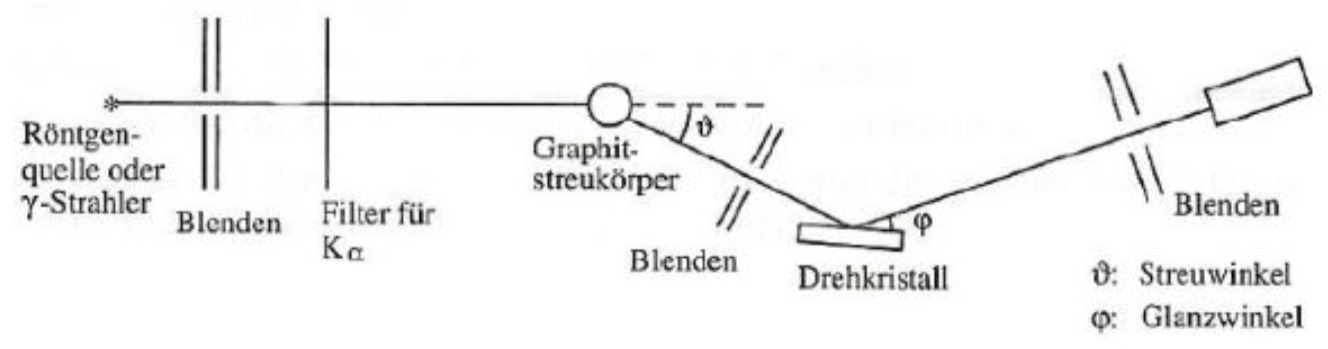
-
Bei einer Messung mit einem Winkel von
tritt Strahlung auf, deren Wellenlänge sich durch den Streuprozess verdoppelt hat. Berechnen sie die Frequenz der einfallenden Strahlung. -
Berechnen sie nun die Geschwindigkeit des gestreuten Elektrons. Ist eine relativistische Rechnung notwendig ?
Lösungsweg:
a) Wellenlänge zum Freischlagung eines Elektrons:
Es wird eine Energie von
b) Frequenz der einfallenden Strahlung
Die Compton Beziehung besagt
Da sich die Wellenlänge verdoppelt hat, gilt für die ursprüngliche Wellenlänge
Somit ist die Frequenz:
c) Geschwindigkeit des gestreuten Elektrons
Aufgrund der Energieerhaltung ist die kinetische Energie des Elektrons nach dem Stoß:
Da dies ähnlich groß wie die Ruhemasse eines Elektrons (511 keV) ist, muss relativistisch gerechnet werden
Mit