Aufgabenstellung:
Gegeben sei folgende Regelstrecke:
Störungen treten vor allem im Frequenzband
Ein Regler soll so ausgelegt werden (nicht Teil dieser Aufgabe), dass ein stabiler geschlossener Regelkreis resultiert und dass Störungen
Existiert ein Regler
Lösungsweg:
Die Störungen im genannten Frequenzbereich müssen durch das Regelsystem um den Faktor 10 reduziert werden. Für die Durchtrittsfrequenz
Das Rauschen ist sehr hochfrequent
Um die Regelstrecke im Frequenzbereich analysieren zu können, muss zuerst die Übertragungsfunktion des Systems
Es gibt mehrere Möglichkeiten
- Laplace-Transformation aller Gleichungen (mit Annahme
), Auflösen des linearen Gleichnugssystems. - Bestimmen der Zustandsraumdarstellung des Systems, Berechnen der Übertragungsfunktion mit
. - Sehen, dass die Struktur der Systemmatrizen der Reglernormalform entspricht. Entsprechend kann daraus direkt die Übertragungsfunktion abgelesen werden.
Exemplarisch wird die 2. Vorgehensweise aufgezeigt.
Mit der Totzeit ergibt sich die Übertragungsfunktion
Einschränkungen durch instabile Pole
Die betrachtete Strecke hat einen instabilen Pol bei
Einschränkungen durch nicht-minimalphasige Nullstellen
Die betrachtete Regelstrecke hat eine nicht-minimalphasige Nullstelle bei
Einschränkungen durch Totzeit
Die Totzeit beschränkt die Durchtrittsfrequenz ebenfalls von oben. Es muss gelten:
Einschränkungen durch Modellunsicherheit
Aus der Übertragungsfunktion
Die folgende Abbildung zeigt die besprochenen Frequenzverhältnisse.
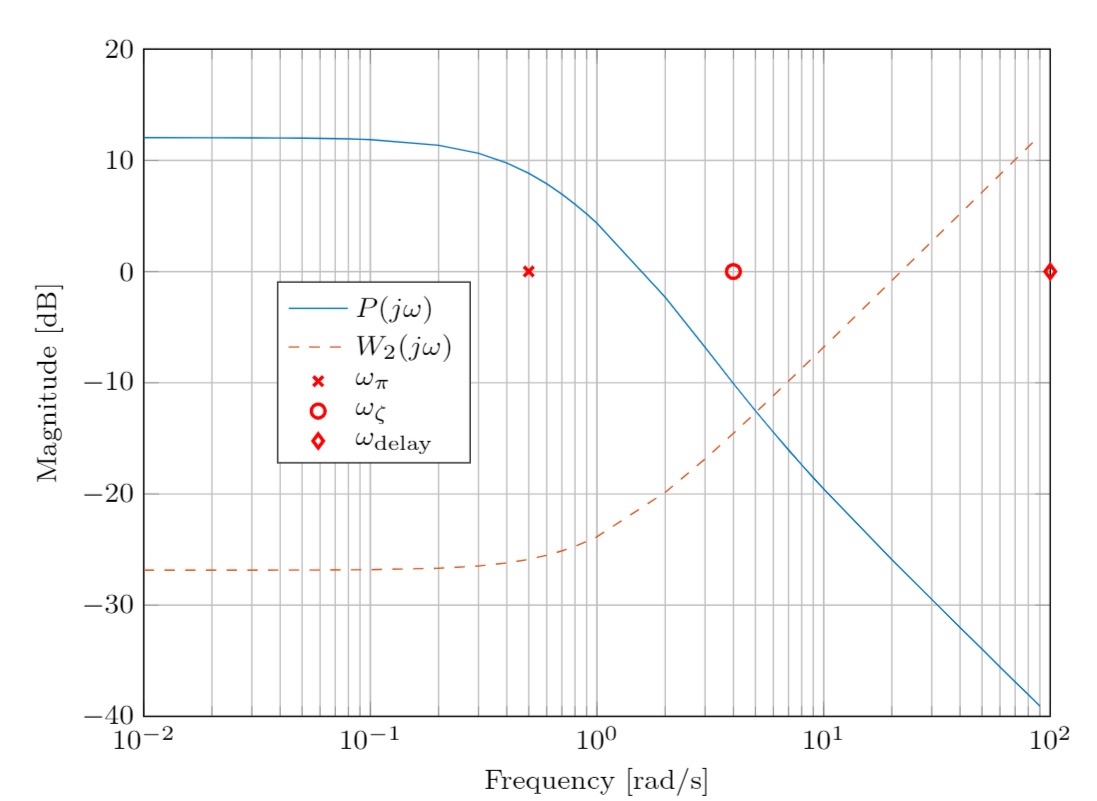
Schlussfolgerung: Zusammengefasst ergeben die obigen Bedingungen die folgende Ungleichnung:
Diese Ungleichung kann erfüllt werden. Somit kann ein Regler gefunden werden. Das Frequenzband ist allerdings sehr eng. Für konservativere Auslegungen (z.B. Faktor 5 anstatt 2) kann kein Regler gefunden werden.
Lösung:
siehe Musterlösung