Aufgabenstellung:
Gegeben ist das folgende System in Blockschaltbild-Form
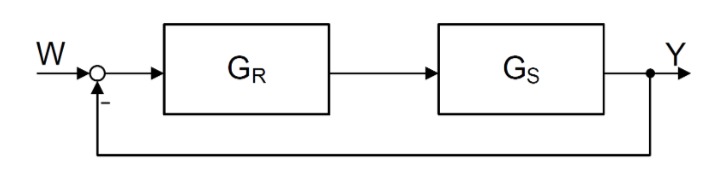
mit den beiden Übertragungsfunktionen
Schließen Sie den Regelkreis in beiden Fällen mit einen P-Regler
Lösungsweg:
Betrachtung von Übertragungsfunktion (1)
Laut Aufgabenstellung wird ein Standardregelkreis mit einem P-Regler
Da im Rückkopplungspfad keine Übertragungsfunktion vorhanden ist, gilt
Für den Nenner ergibt sich
Somit ergibt sich für
Um einen Bereich für
Nach der notwendingen Bedingung für Stabilität müssen alle Koeffizienten
Zusätzlich müssen für die hinreichende Bedingung für Stabilität nach Hurwitz noch die Determinanten der beiden Hurwitz-Matrizen geprüft werden.
Die Matrix
Für Stabilität muss die Determinante von
Somit ist der geschlossene Regelkreis nur genau dann stabil, wenn für
gewählt wird.
Betrachtung von Übertragungsfunktion (2)
Analog zur vorherigen Aufgabe wird ein Standardregelkreis mit einem P-Regler betrachtet, somit gilt
Da
Daraus folgt für den Nenner der Übertragungsfunktion
Daraus folgt für die vollständige Übertragungsfunktion des geschlossenen Regelkreises
Durch die zusätzliche Nullstelle
Um den Bereich für
Damit der geschlossene Regelkreis stabil ist, müssen alle Koeffizienten
Daraus folgt für
Für Stabilität müssten beide Bedinungen erfüllt sein, somit ist der geschlossene Regelkreis nur für
Zusätzlich müssen noch die Determinanten der Hurwitz Matrizen geprüft werden.
Für die Determinante von
Für
Für Stabilität muss die Determinante von
Da diese Bedingung bereits durch die vorher aufgestellte Bedingung
Lösung:
Übertragungsfunktion (1):
Übertragungsfunktion (2):