3 / 19

Aufgabenstellung:

Von einer Regelstrecke sind die Ortskurve und die Pol- und Nullstellenverteilung bekannt:

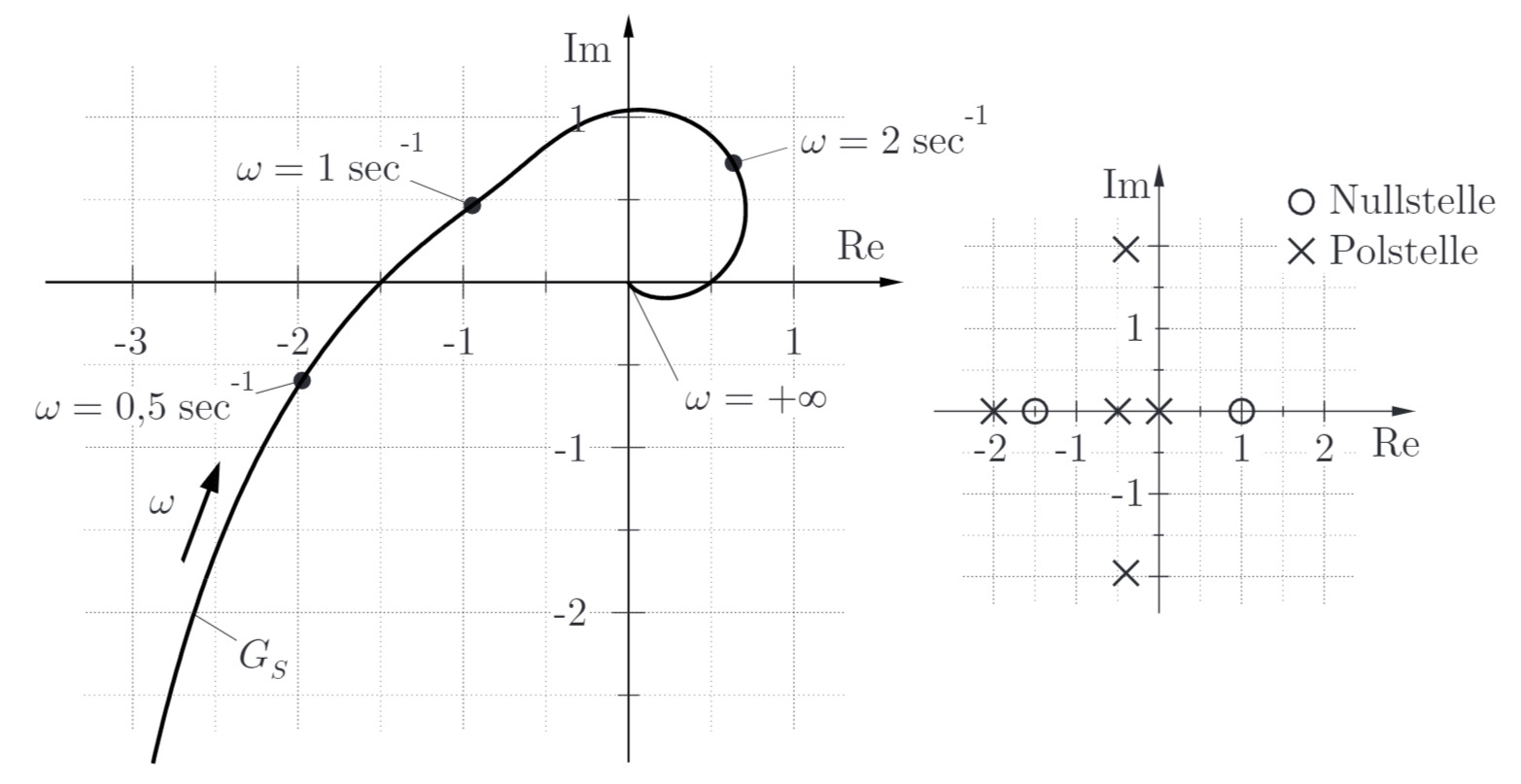
Abbildung

a) Ist die Regelstrecke schwingungsfähig? Begründen Sie Ihre Antwort.
b) Bestimmen Sie das Ausgangssignal im eingeschwungenen Zustand, wenn die Regelstrecke mit dem Eingangssignal angeregt wird.
c) Die Regelstrecke soll mit einem -Regler geregelt werden. Das vereinfachte Nyquist-Kriterium ist anwendbar. Bestimmen Sie so, dass der geschlossene Regelkreis eine Amplitudenreserve aufweist.


Nun gilt

 

d) Welche Phasenreserve liegt mit diesem vor?

 

Betrachtet wird ein System mit der Übertragungsfunktion

 

e) Zeigen Sie, dass das System stabil ist.
Das System wird nun mit dem Eingangssignal beaufschlagt.

f) Bestimmen Sie den statischen Endwert .

 

Hinweis: Alle Aufgabenteile sind unabhängig voneinander lösbar.

Lösungsweg:

Drücke auf "Aufdecken" um dir den ersten Schritt der Lösung anzuzeigen

a) Schwingfähigkeit 

Ja, die Regelstrecke ist schwingungsfähig, da ein komplex konjugiertes Polpaar vorliegt.

b) Bestimmung von

Betrag und Phase aus der Ortskurve bei ablesen ergibt:

Daraus folgt für das Ausgangssignal:

c) Bestimmung von

Es gilt:

Ablesen von aus der Ortskurve führt schließlich zu:

d) Phasenreserve  

Da der P-Regler keine Phasenveränderung bewirkt, kann hier alternativ zur Bestimmung des Schnittpunktes der Ortskurve von mit dem Einheitskreis auch der Schnittpunkt der Ortskurve von mit einem Kreis mit Radius 3 um den Ursprung bestimmt werden.

Für ergibt sich:

e) Stabilität

Anwenden des algebraischen Stabilitätskriteriums nach Hurwitz auf das Nennerpolynom:

1. Bedingung: 

Alle Koeffizienten vorhanden und positiv
die Bedingung ist erfüllt

2. Bedingung: 

Für das Polynom 3. Ordnung muss folgende Ungleichung erfüllt sein:

die Bedingung ist erfüllt

Das System ist stabil.

f) statischer Endwert

Der statische Endwert kann über den Grenzwertsatz bestimmt werden. Die Anwendbarkeit ist gegeben. da das System stabil ist.

Lösung:

  1. Die Regelstrecke ist schwingungsfähig

  5. Das System ist stabil