Aufgabenstellung:
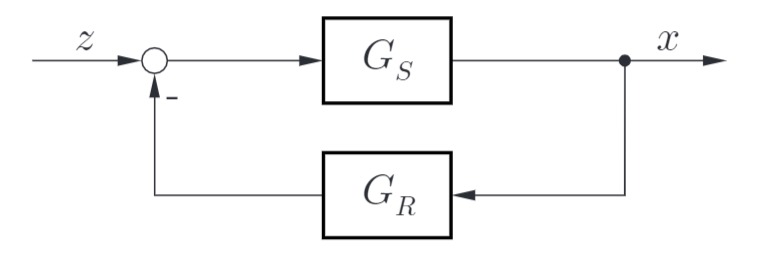
Betrachtet wird der folgende Regelkreis
Die Ortskurve des Frequenzgangs von
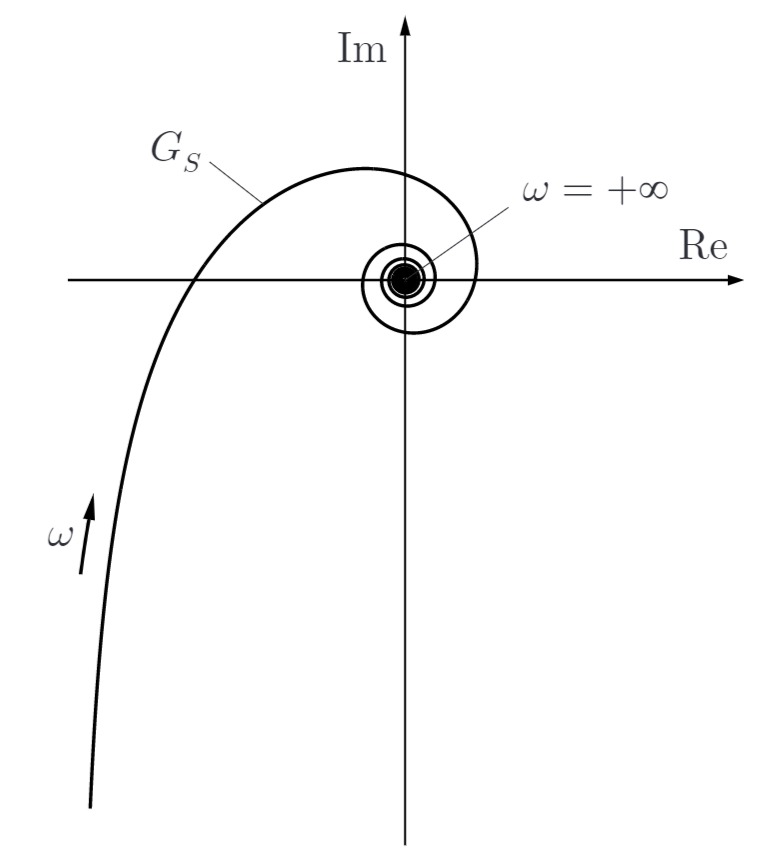
a) Begründen Sie, warum der geschlossene Regelkreis mit einem
Nun soll ein
b) Bestimmen Sie die Reglerparameter
Lösungsweg:
a) Begründen, warum der geschlossene Regelkreis mit einem
Bedingungen für die Anwendbarkeit des vereinfachten Nyquist-Kriteriums prüfen:
1.
2. Die Phase von
Beide Bedingungen sind damit erfüllt.
Für kleine
b) Reglerparameter
Bestimmen von
Daraus folgt für
Eingesetzt folgt für
Nach den Einstellregeln nach Ziegler und Nichols folgt somit für einen
Lösung:
- Der geschlossene Regelkreis ist für kleine
stabil. -