3 / 4

Aufgabenstellung:

Der Antriebsstrang eines elektrischen Fahrzeugs soll modelliert werden. Die vereinfachte Struktur des Antriebsstrangs ist nachfolgend dargestellt.

Abbildung

Hierbei bezeichnet die Eingangsspannung des Gleichstrommotors, die Größe bezeichnet das Drehmoment des Motors und bezeichnet das Moment nach der Übersetzung durch das Getriebe. Mit wird die Geschwindigkeit des Fahrzeugs bezeichnet. Des Weiteren wird der Gleichstrommotor durch das dargestellte Ersatzschaltbild beschrieben.

Abbildung

Mit und wird die Ankerinduktivität und der Ankerwiderstand bezeichnet. Die Größe bezeichnet die durch die Winkelgeschwindigkeit der Motorachse erzeugte induzierte Gegenspannung. Das Motormoment ergibt sich durch .
Das Getriebe übersetzt das vom Motor erzeugte Drehmoment mit dem Verhältnis nach der Formel , wobei das Moment direkt auf die Antriebsachse übertragen wird. Das Fahrzeug selbst besitzt die Masse und einen Raddurchmesser , wobei die Räder ideal abrollen. Elastizitäten, Reibungseinflüsse sowie die Trägheitsmomente der Räder können vernachlässigt werden.

  1. Bestimmen Sie mit Hilfe des Ersatzschaltbildes eine Differentialgleichung, die die Dynamik des Elektromotors beschreibt und stellen Sie diese Differentialgleichung in Form eines Blockschaltbildes dar. Behandeln Sie die Winkelgeschwindigkeit zunächst als zusätzliche unabhängige Eingangsgröße.
  2. Bestimmen Sie eine Differentialgleichung die das dynamische Verhalten des Getriebes und der Fahrzeugdynamik beschreibt und stellen Sie diese ebenfalls als Blockschaltbild dar.
  3. Stellen Sie das gesamte modellierte System in einem Blockschaltbild dar und ergänzen Sie die für das Motormodel benötigte Rückführung der Winkelgeschwindigkeit aus der Fahrzeugdynamik.
  4. Fügen Sie das modellierte System in einen geschlossenen Standardregelkreis ein. Dabei stellt die Eingangsspannung die Stellgröße und die Fahrzeug-Geschwindigkeit die Regelgröße dar. Der Regler und die Messeinrichung können als allgemeine Blöcke eingetragen werden.

Lösungsweg:

Drücke auf "Aufdecken" um dir den ersten Schritt der Lösung anzuzeigen

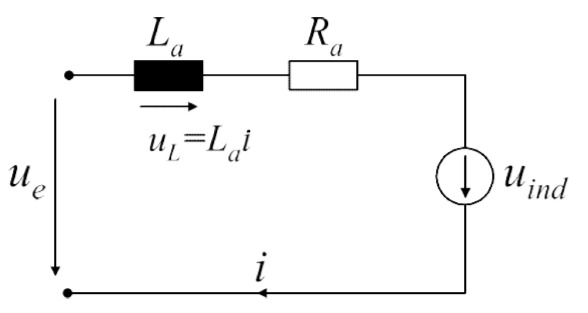
a) Gesucht ist die Differentialgleichung für , was dem Ausgang des Teilsystems Elektromotor entspricht.

Als Eingang fungiert die anliegende Eingangsspannung . Aus der Kirchhoffschen Maschengleichung ergibt sich

Weiterhin gilt für die elektrischen Bauteile (Induktivität und ohmscher Widerstand)

  • Induktivität:
  • Ohmscher Widerstand:

Somit folgt

beziehungsweise

Aus der Aufgabenstellung folgt, dass beziehungsweise gilt. Somit ergibt sich die gesuchte DGL zu

Blockschaltbild:

Abbildung

b) Differentialgleichung die das dynamische Verhalten des Getriebes und der Fahrzeugdynamik beschreibt und Blockschaltbild

Im nächsten Schritt wird das Getriebe und die Fahrdynamik modeliert. Mit den Angaben der Aufgabenstellung ergibt sich

Getriebe: (1)

Kraftübertragung Straße: (2)

Dynamik Fahrzeugmasse: (3)

Durch Einsetzen von (1) in (2) und dem Einsetzen des Ergebnisses in (3) ergibt sich die DGL

Blockschaltbild:

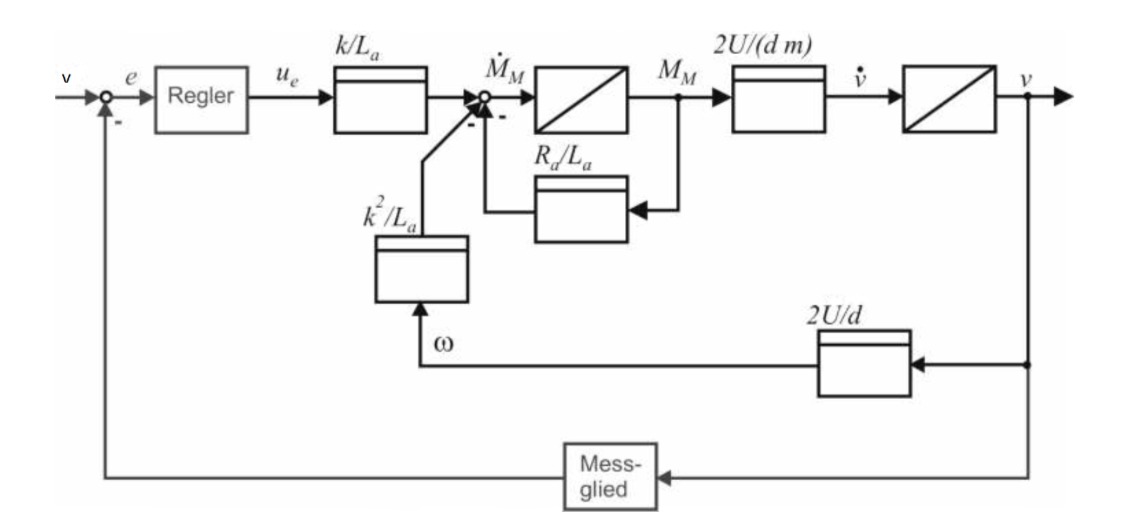
Abbildung

c) Gesamte System in Blockschaltbild

Zunächst muss die Winkelgeschwindigkeit (Motordrehzahl) aus der Fahrtgeschwindigkeit ermittelt werden. Es gilt für die Raddrehzahl

Mit Hilfe der Getriebeübersetzung lässt sich diese Drehzahl dann auf die Motordrehzahl umrechnen, sodass gilt

Damit ergibt sich das Blockschaltbild des vollständigen Systems zu:

Abbildung

d) Geschlossener Regelkreis (Blockschaltbild):

Abbildung

Lösung:

  3. siehe Musterlösung
  4. siehe Musterlösung