11 / 13

Aufgabenstellung:

Gegeben ist der nachfolgende Wirkungsplan eines physikalischen Systems.

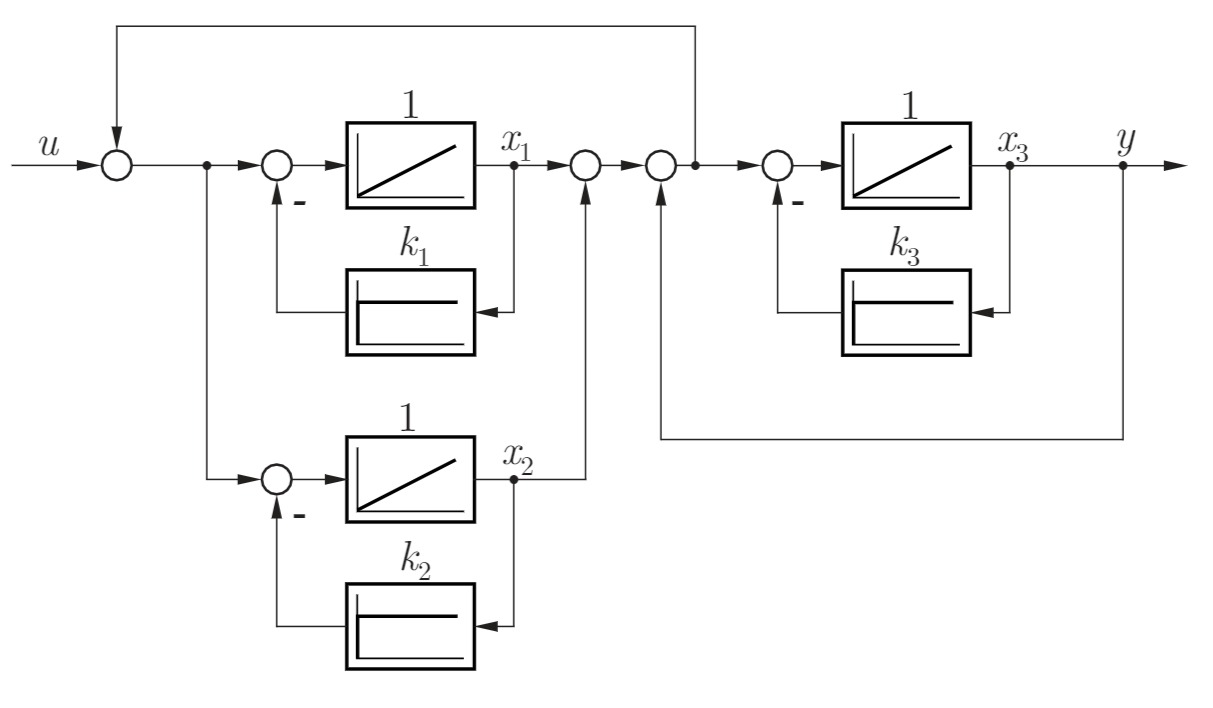
Abbildung

a) Ist das Übertragungssystem sprungfähig?
b) Geben Sie die Zustandsraumdarstellung mit dem Zustandsvektor in der folgenden Form an:

Für eine bestimmte Parametrierung ergibt sich die folgende Systemmatrix , die im Weiteren verwendet werden soll:

c) Ist das Zustandsraummodell stabil?

Übernehmen Sie in der folgenden Teilaufgabe die Vektoren und den Skalar unverändert aus Aufgabenteil b).


d) Ist das physikalische System vollständig steuer- bzw. beobachtbar?

Hinweis: Die Determinante einer - Matrix lässt sich wie folgt berechnen:

Lösungsweg:

Drücke auf "Aufdecken" um dir den ersten Schritt der Lösung anzuzeigen

a) Sprungfähigkeit von

Das System ist nicht sprungfáhig, da nur verzögert auf wirkt.

b) Zustandsraumdarstellung

Für den gegebenen Zustandsvektor kann die Zustandsraumdarstellung direkt aus dem Wirkungsplan abgelesen werden:

c) Stabilität

Berechnen des char. Polynoms:

Für den Koeffizienten gilt . Daher ist die notwendige Bedingung nach Hurwitz nicht erfüllt.

System ist nicht stabil.

d) Steuer- und Beobachtbarkeit

Aufstellen der Steuerbarkeitsmatrix:

nicht steuerbar

Aufstellen der Beobachtbarkeitsmatrix:

beobachtbar

Lösung:

  1. nicht sprungfähig

  3. nicht stabil
  4. nicht steuerbar; beobachtbar