2 / 4

Aufgabenstellung:

Gegeben ist ein System in dimensionsloser Zustandsraumdarstellung mit der Systemmatrix

und dem Eingangsvektor .

a) Bestimmen Sie mit Hilfe der Routhschen Probefunktionen die Anzahl der Eigenwerte von mit positivem Realteil. Ist das System stabil?

Es soll nun eine Zustandsrückführung ausgelegt werden. Das System mit Zustandsrückführung soll folgende Polstellen aufweisen:

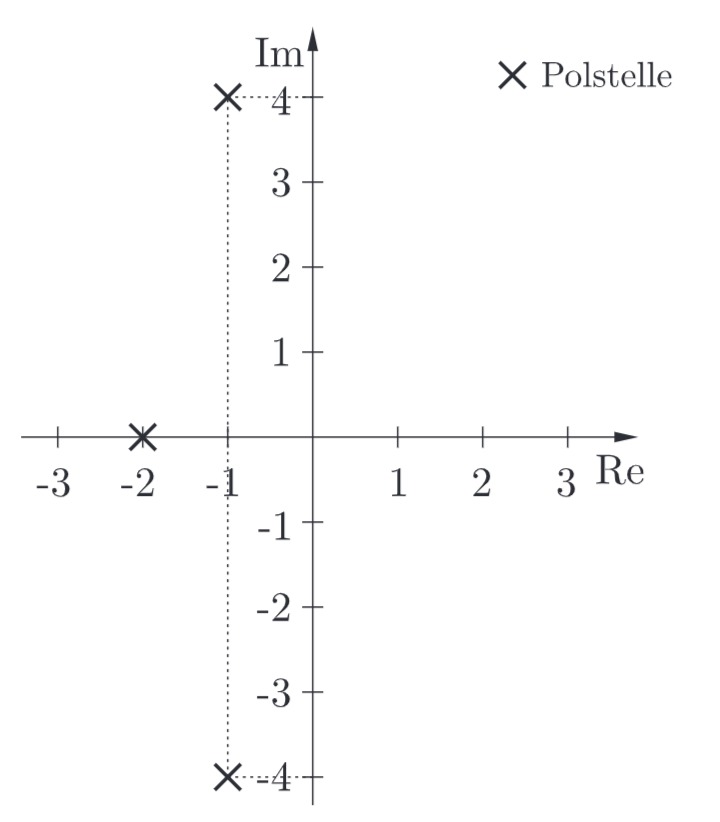
Abbildung

b) Nennen Sie einen Nachteil, den die gegebene Wahl der Polstellen für das Systemverhalten hat.
c) Bestimmen Sie .

 

Hinweis: Alle Aufgabenteile können unabhängig voneinander gelöst werden.

Lösungsweg:

Drücke auf "Aufdecken" um dir den ersten Schritt der Lösung anzuzeigen

a) Stabilität 

Charakteristisches Polynom bestimmen:

Aussage zu Stabilität

das System ist instabil

Bestimme die Routhschen Probefunktionen:

Anzahl der Vorzeichenwechsel in der Folge der Routhschen Probefunktionen: 1

Anzahl der Eigenwerte von mit positivem Realteil: 1

Das System weist einen Eigenwert mit positivem Realteil auf und ist daher instabil.

b) Nachteil bei der Wahl der Polstellen 

Das System weist eine geringe Dämpfung auf (starkes Überschwingen bei sprungförmiger Anregung).

c)

Zustandsraumdarstellung mit Zustandsrückführung:

Charakteristisches Polynom:

Bestimme Sollpolynom:

Polstellen aus Diagramm:

Sollpolynom:

Koeffizientenvergleich mit charakteristischem Polynom

Lösung:

  1. Anzahl der Eigenwerte: 1 ; instabil 
  2. siehe Musterlösung