1 / 4

Aufgabenstellung:

Für einen Helikopter soll eine Positionsregelung entworfen werden (mit Position und Neigungswinkel ) :

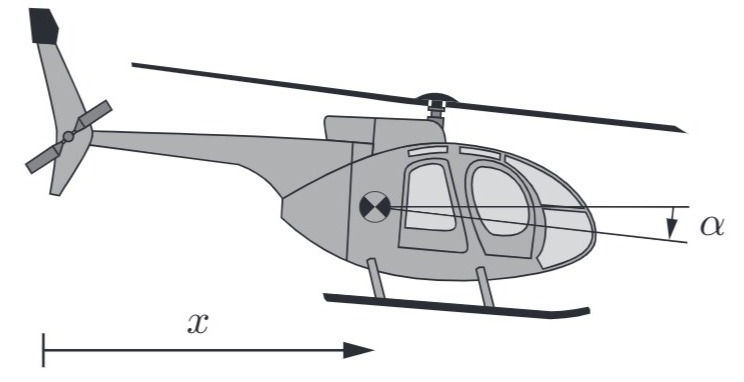
Abbildung

 

Das Regelsystem mit Führungsgröße kann durch folgenden Wirkungsplan beschrieben werden:

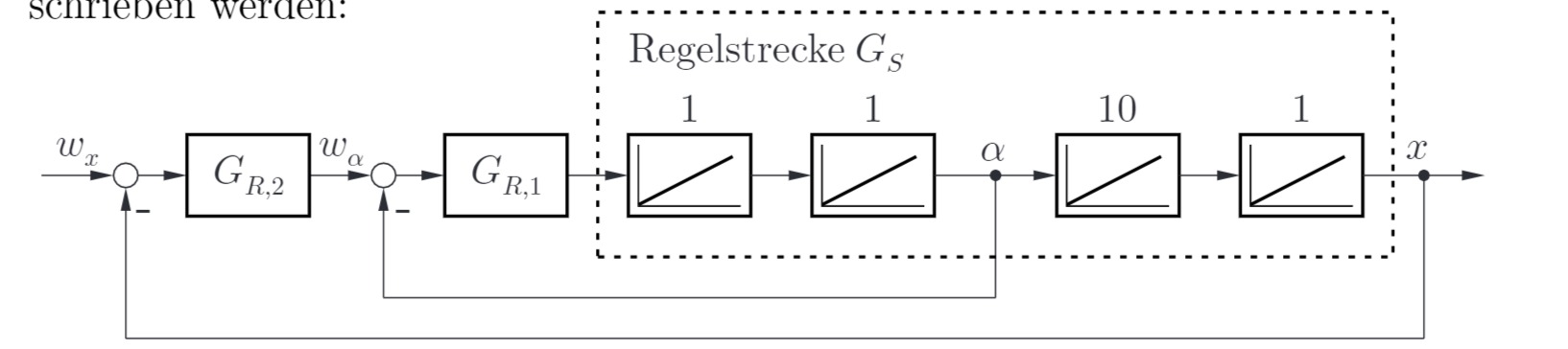
Abbildung

Hinweis: Alle Aufgabenteile sind unabhängig voneinander lösbar.

a) Begründen Sie, warum eine Positionsregelung mit einem einzelnen PIDRegler ohne unterlagerte Nickregelung den geschlossenen Regelkreis nicht stabilisieren kann.

Zunächst soll ein -Regler ausgelegt werden.

b) Bestimmen Sie die Reglerparameter und so, dass der geschlossene innere Regelkreis Polstellen entsprechend dem gegebenen Pol-Nullstellen Diagramm aufweist.

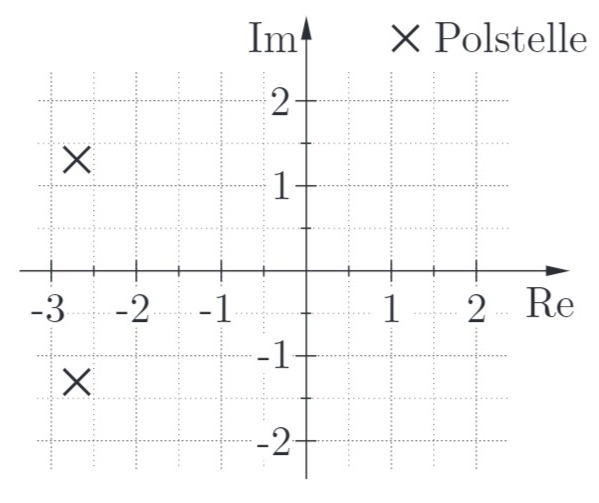
Abbildung

Für den äußeren Regelkreis wurde ein weiterer -Regler ausgelegt. Die Übertragungsfunktion des geschlossenen Regelkreises lautet:

c) Bestimmen Sie die Routhschen Probefunktionen von . Ist stabil?
d) Der statische Endwert von für einen Einheitssprung beträgt Warum gibt es hier trotz fehlendem -Anteil im Regler keine bleibende Regelabweichung?

Lösungsweg:

Drücke auf "Aufdecken" um dir den ersten Schritt der Lösung anzuzeigen

a) Begründung: nicht stabilisierbar

Aufstellen der Übertragungsfunktion des geschlossenen Regelkreises mit und

Die Koeffizienten für und des Nennerpolynoms sind nicht vorhanden. Damit ist die 1 . Bedingung des Hurwitz-Kriteriums nicht erfüllt, sodass der geschlossene Regelkreis für beliebige Reglerparameter instabil ist.

b) Reglerparameter und nach Pol-Nullstellen-Diagramm

Aus dem Pol-Nullstellen Diagramm lassen sich die Dämpfung und die Kennkreisfrequenz für ein -Element ablesen:

Daraus ergibt sich das gewünschte Nennerpolynom:

Aufstellen der Übertragungsfunktion des geschlossenen inneren Regelkreises mit und ergibt:

Ein Koeffizientenvergleich mit dem Nennerpolynom ergibt:

c) Routhschen Probefunktionen und Stabilität

Untersucht wird das Nennerpolynom. Aufstellen des Routh-Schemas:

Abbildung

Bedingungen für Stabilität des geschlossenen Regelkreises:

  1. Alle Koeffizienten vorhanden und positiv Bedingung erfüllt
  2. Alle Routhschen Probefunktionen gröfer als null Bedingung erfüllt ist stabil.

d) Begründung: Warum keine bleibende Regelabweichung?

Der aufgeschnittene Positionsregelkreis hat bereits ohne I-Anteil im Regler integrierendes Verhalten. Damit gibt es im Führungsübertragungsverhalten keine bleibende Regelabweichung.

Lösung:

  1. Die 1 . Bedingung des Hurwitz-Kriteriums ist nicht erfüllt [\rightarrow\] instabil 

  2. ;

  3. ist stabil
  4. Aufgrund des integrierenden Verhaltens.