3 / 7

Aufgabenstellung:

Von einem B/E-Netz sind der abgebildete Erreichbarkeitsgraph sowie das abgebildete Petri-Netz , in welchem die Benennung der Stellen und Transitionen sowie die Anfangsmarkierung noch fehlen, gegeben. Das Netz arbeitet nach der starken Schaltregel.

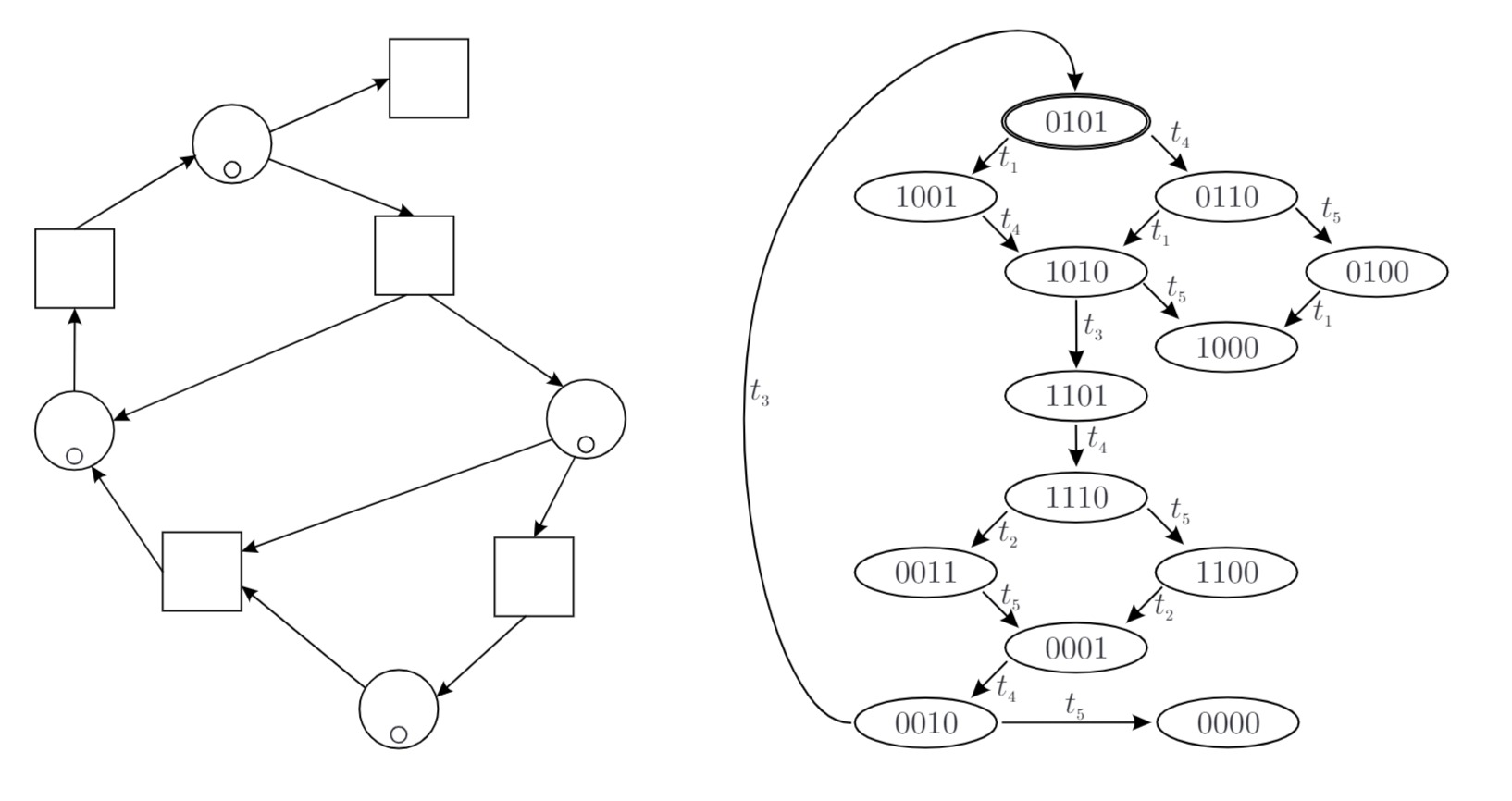
Abbildung

a) Vervollständigen Sie das Petri-Netz .

b) Ermitteln Sie eine unter der Anfangsmarkierung anwendbare Schaltsequenz, die das Netz in den Anfangszustand zurückführt.

c) Stellen Sie die Netzmatrix auf und weisen Sie nach, dass die Transitionsfolge aus Aufgabenteil b) einer T-Invariante des Netzes entspricht.

 

Hinweis: Die folgenden Aufgabenteile sind unabhängig von den vorherigen lösbar.

Das gegebene System beschreibt einen Produktionsprozess, welcher wiederholt ablaufen soll.

d) Welche Transition gefährdet potentiell das wiederholte Ablaufen des Produktionsprozesses?

 

In einem Lehrbuch steht, dass verschiedene Petri-Netze denselben Erreichbarkeitsgraphen besitzen können.

e) Erweitern Sie um eine weitere Stelle und/oder eine Transition, ohne den Erreichbarkeitsgraphen zu ändern.

Lösungsweg:

Drücke auf "Aufdecken" um dir den ersten Schritt der Lösung anzuzeigen

a) Petri-Netz

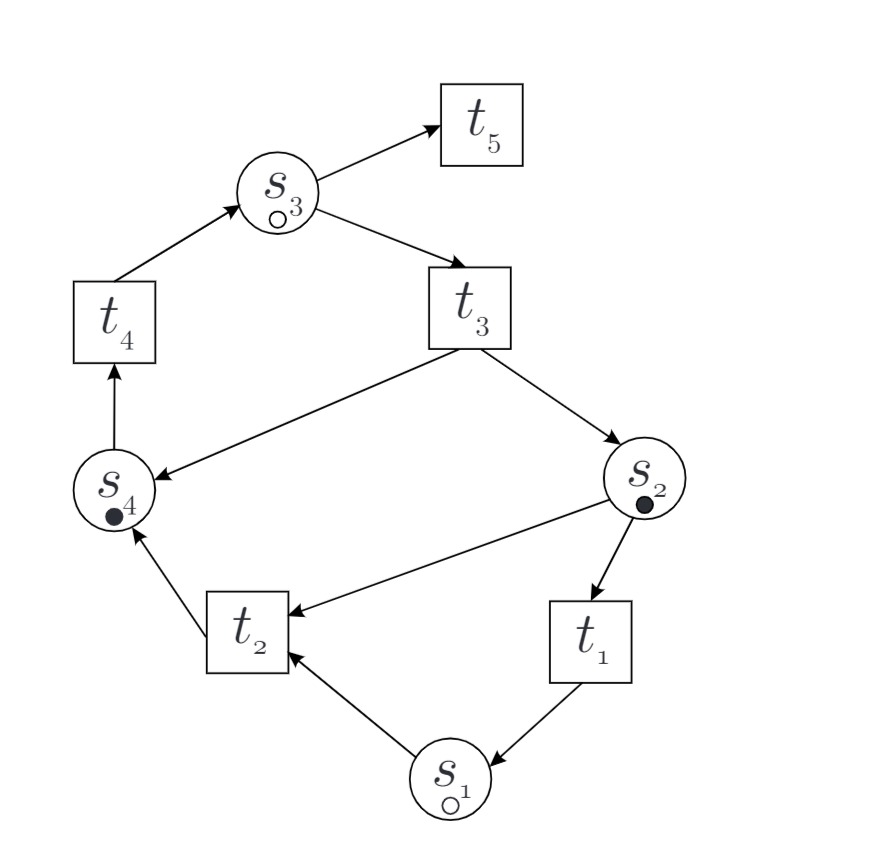
Abbildung

b) Schaltsequenz

Eine mögliche Transitionsfolge lautet

c) Nachweis T-Invariante

Netzmatrix

T-Invariante

Zählen der Transitionshäufigkeiten im Ergebnis aus b) liefert

Es gilt

Somit ist eine T-Invariante des Netzes.

d) Welche Transition gefährdet potentiell das wiederholte Ablaufen des Produktionsprozesses?

, da es zu einer totalen Verklemmung kommt, wenn diese Transition bspw. bei der erreichbaren Markierung (0010) schaltet.

e) erweiern

Das Hinzufügen beliebiger Stellen ergänzt die Markierungs-Zahlentupel um eine Ziffer und ändert somit die Knoten des Erreichbarkeitsgraphen. Es kommt also nur eine Transition in Frage, die so gewählt werden muss, dass sie unter keinen Umständen schaltfähig ist. Da beispielsweise die Markierung (1111) nicht erreichbar ist, lautet eine Möglichkeit für die Wahl von :

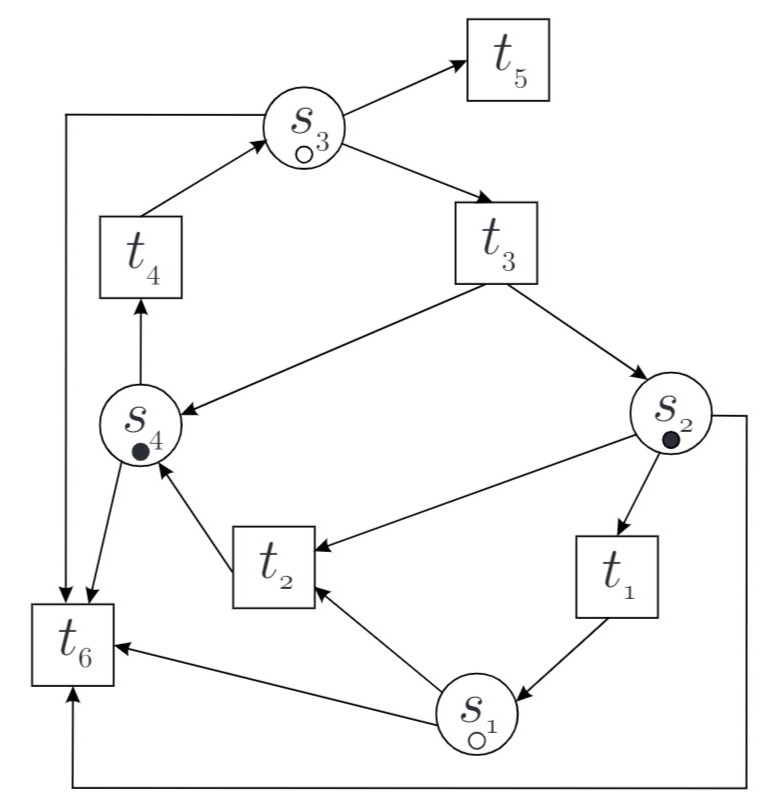
Abbildung

Lösung:

  1. siehe Musterlösung



  3. ;  ist eine T-Invariante des Netzes.



  5. siehe Musterlösung