9 / 9

Aufgabenstellung:

Betrachtet wird der folgende Regelkreis:

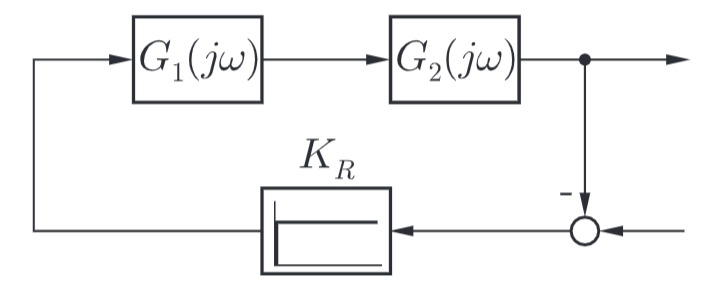
Abbildung

mit

und ist minimalphasig.


Der Phasengang von des aufgeschnittenen Regelkreises ist im Bodediagramm gegeben.

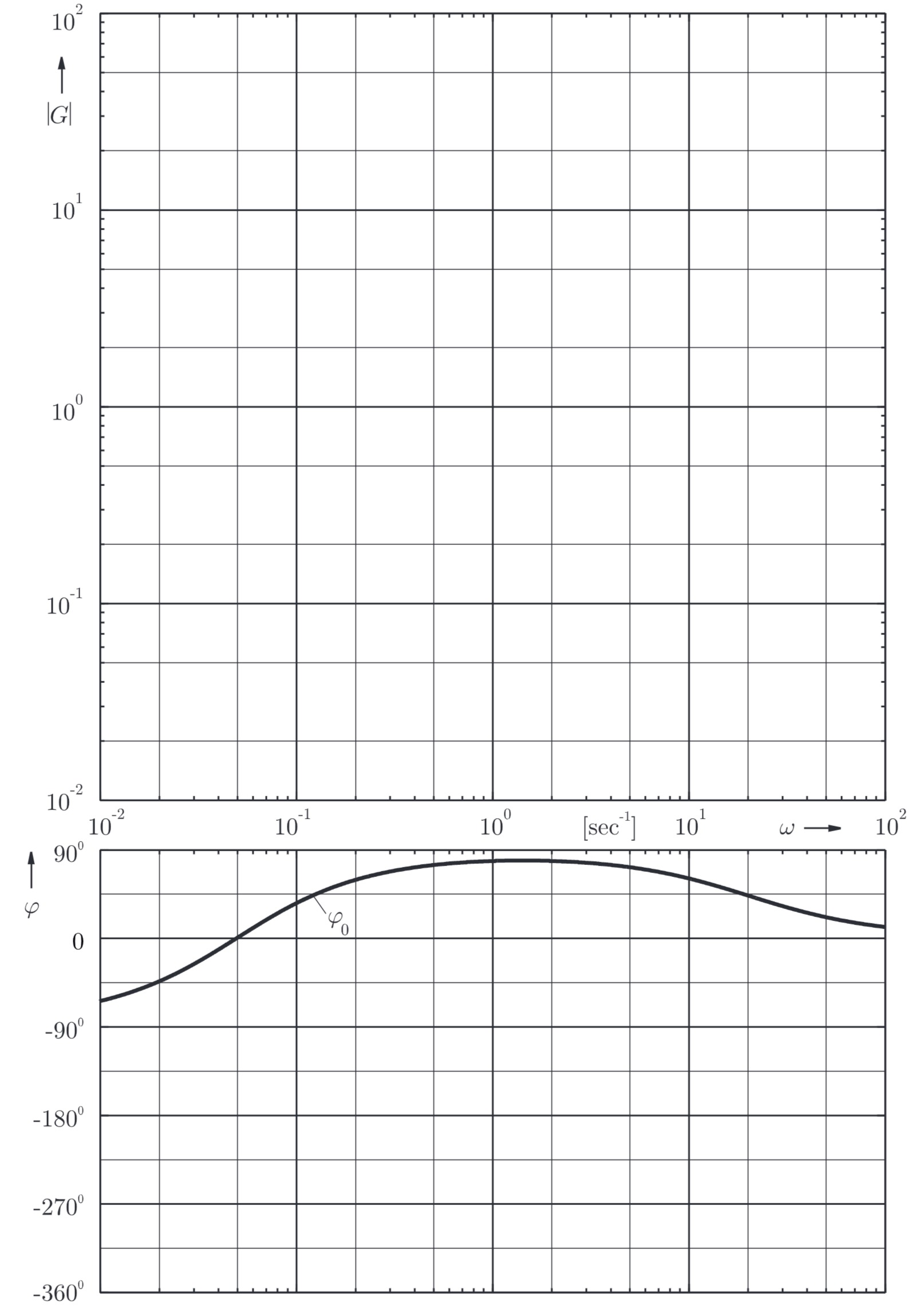
Abbildung

a) Konstruieren Sie den Amplitudengang für . Die Darstellung der Asymptoten ist ausreichend.

wird nun durch ersetzt:

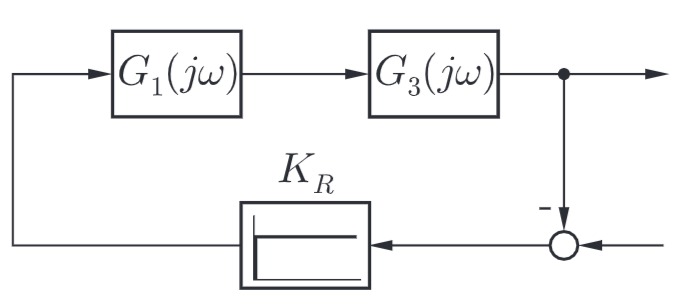
Abbildung

mit .

b) Bestimmen Sie so, dass die Amplitudenreserve des geschlossenen Regelkreises beträgt. Für den Betragsverlauf genügt die Betrachtung der Asymptoten.

Lösungsweg:

Drücke auf "Aufdecken" um dir den ersten Schritt der Lösung anzuzeigen

a) Amplitudengang

Abbildung

aus :

aus Phasenverlauf :

und minimalphasig :

mit

aus Wendepunkt bei von :

Asymptoten einzeichnen.

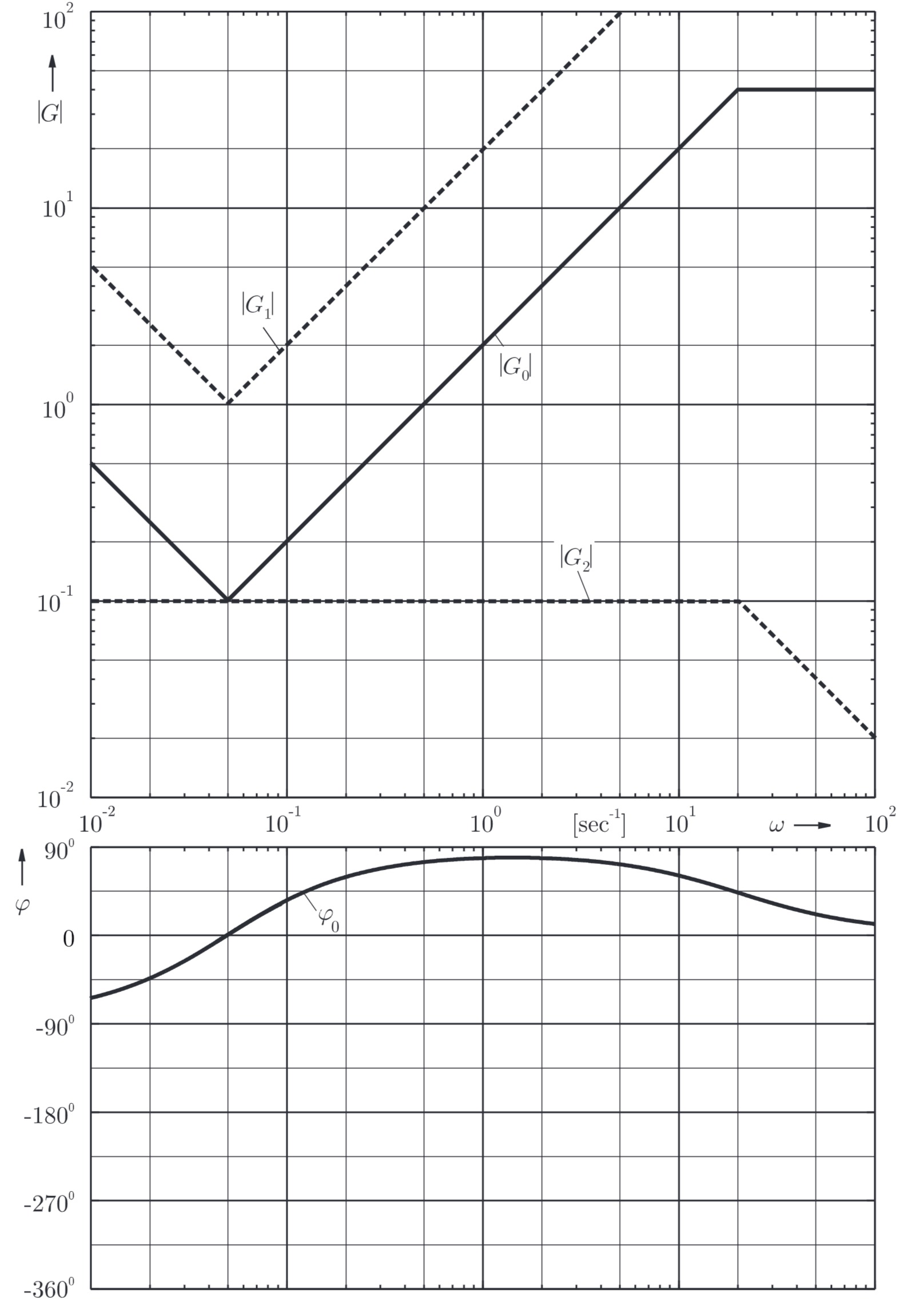
Abbildung

b)

hat integrierendes Verhalten und schneidet die Linien im Bode-Diagramm ausschließlich mit negativer Steigung Vereinfachtes Nyquist-Kriterium anwendbar!

Betrachte für Stabilität:

aus Bodediagramm:

Hinweis: Die Ortskurve des Frequenzgangs schneidet die reele Achse undendlich oft bei . Aus dem Amplitudengang folgt daraus, dass stabilitätsentscheidend ist.

Lösung:

  1. siehe Musterlösung