8 / 9

Aufgabenstellung:

Betrachtet wird die folgende Regelstrecke:

Abbildung

mit .

Der Frequenzgang von ist im Bode-Diagramm dargestellt.

Hinweis: In allen Aufgabenteilen ist für den Betragsverlauf die Betrachtung der Asymptoten ausreichend.

a) Bestimmen Sie in der Form:

Die Regelstrecke soll mit einem -Regler mit geregelt werden.

b) Konstruieren Sie den Amplituden- und den Phasenverlauf des aufgeschnittenen Regelkreises im Bode-Diagramm. Bestimmen Sie dabei durch Konstruktion die Zeitkonstante des Reglers so, dass die Ortskurve von durch den im folgenden Diagramm markierten Punkt verläuft.

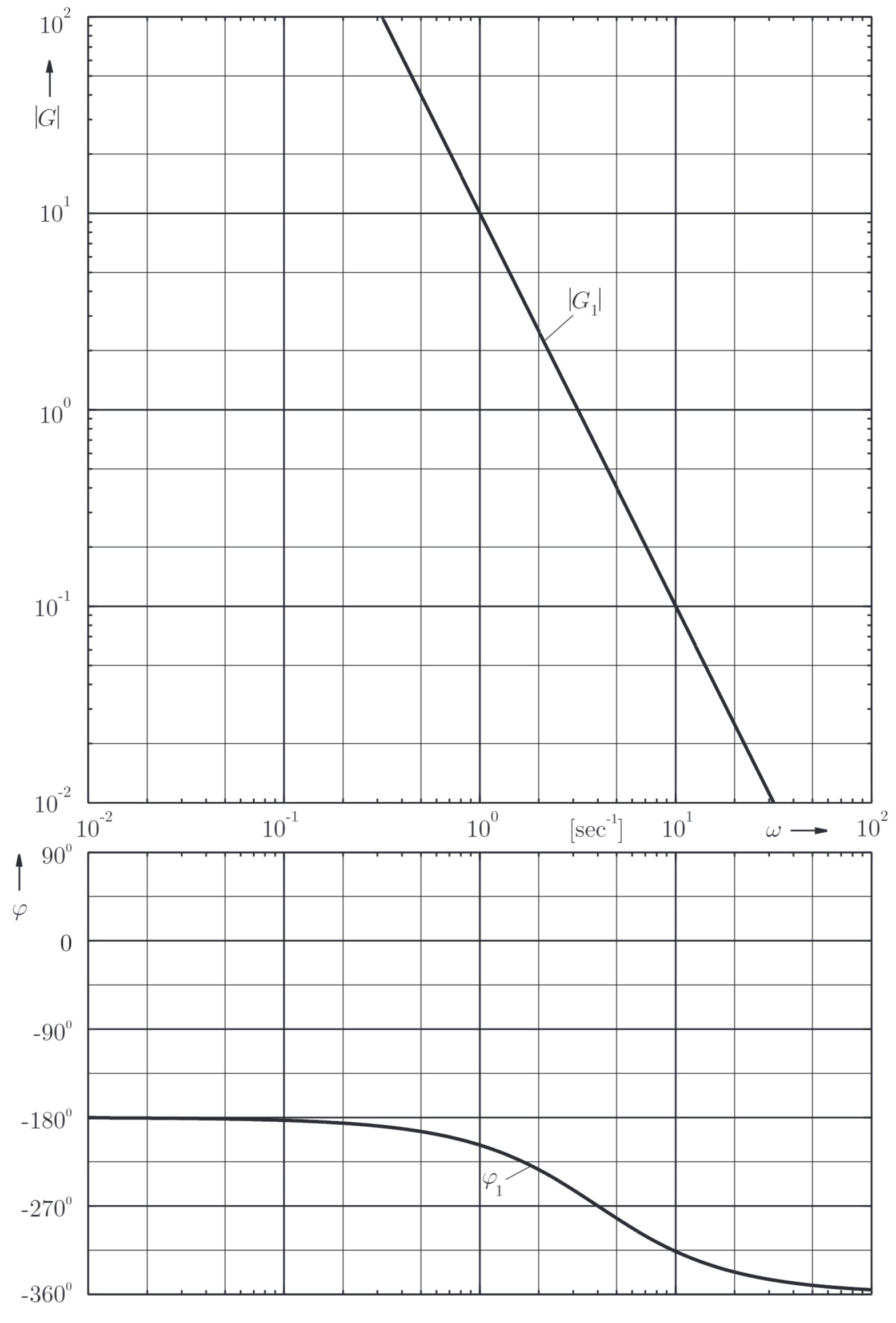
Abbildung

Abbildung

Hinweis: Spalten Sie für die Konstruktion im Bode-Diagramm das -Element in ein - und ein -Element auf.

c) Ist der geschlossene Regelkreis mit dem aus b) stabil? Begründen Sie Ihre Antwort.

Lösungsweg:

Drücke auf "Aufdecken" um dir den ersten Schritt der Lösung anzuzeigen

a)

aus Bode-Diagramm:

ist eine Reihenschaltung aus einem Allpass und zwei Integrierern.

Ablesen der Eckfrequenz des Allpasses:

Ablesen des Integriererbeiwerts (an beliebigem ):

b) Bodediagramm, Zeitkonstante  

Regler

Konstruktion von und .

Addition der Betrags- und Phasenverläufe zu:

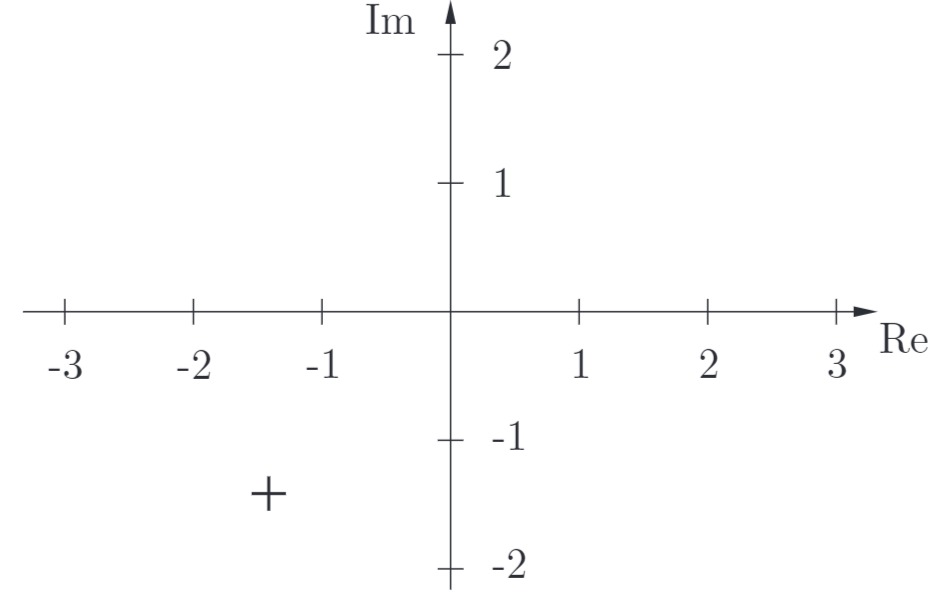
aus Ortskurve : .

Da und für alle muss sein!

(Asymptotenbetrachtung)

ablesen:

aus Korrekturtabelle oder:

in Betrag und Phase konstruieren.

Bodediagramm:

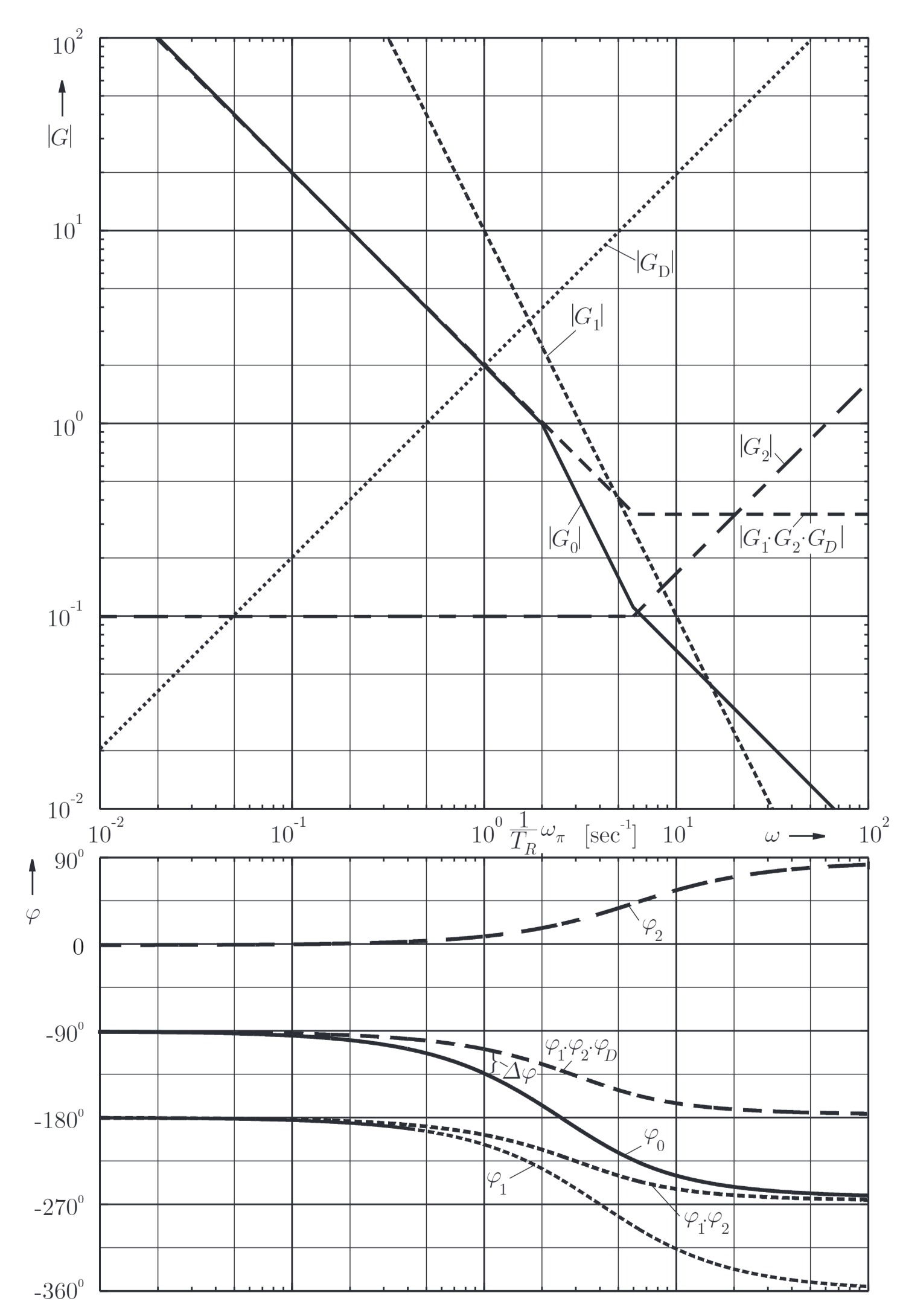
Abbildung

c) Stabilität

Vereinfachtes Nyquist-Kriterium anwendbar, da integrierend und Phase monoton fallend. Betrachte

Der geschlossene Regelkreis ist stabil.

Lösung:

  2. siehe Musterlösung,
  3. stabil