18 / 18

Aufgabenstellung:

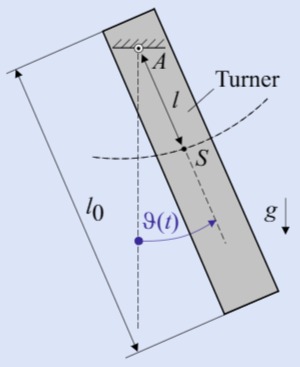
Abbildung

Ein Turner am Reck wird vereinfachend durch einen um die Achse drehbar gelagerten, starren Stab (Länge , Masse , Abstand Drehachse-Schwerpunkt ) modelliert.

  1. Zeigen Sie, dass bzgl. das Trägheitsmoment ist.
  2. Wie lautet die Bewegungsdifferentialgleichung?
  3. Linearisieren Sie die Differentialgleichung (DGL) aus 2. und lösen Sie diese für kleine Auslenkungen .
  4. Wie groß ist die Schwingungsfrequenz der ungedämpften Schwingung?
  5. Um wie viel muss der Turner aus einer völlig gestreckten und waagerechten Anfangslage am unteren Scheitelpunkt den Abstand verringern, damit er gerade einen Überschlag schafft?

Lösungsweg:

Drücke auf "Aufdecken" um dir den ersten Schritt der Lösung anzuzeigen

1. Zeigen Sie, dass bzgl. das Trägheitsmoment ist.

Unter Annahme eines Stabs homogener Dichte ist . Skizze des Turners mit Koordinatensystem im Mittelpunkt und infinitisimalem Flächenelement:

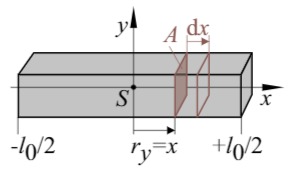
Abbildung

2. Wie lautet die Bewegungsdifferentialgleichung?

Lösung über Drehmomentsatz um oder durch Auswertung der LAGRANGE-Gleichung:

Auswertung der LAGRANGE-Gleichung mit

mit (STEINER-Anteil) und der reduzierten Pendellänge folgt:

3. Linearisieren Sie die Differentialgleichung (DGL) aus 2. und lösen Sie diese für kleine Auslenkungen

Für kleine Auslenkungen ist :

Die Lösung der DGL des ungedämpften Schwingers ist .

Mit den Anfangswerten und berechnen sich Amplitude und Nullphasenwinkel :

4. Wie groß ist die Schwingungsfrequenz der ungedämpften Schwingung

Kennkreisfrequenz:

mit

folgt

Aus der Kennkreisfrequenz kann nun bestimmt werden:

5. Um wie viel muss der Turner aus einer völlig gestreckten und waagerechten Anfangslage am unteren Scheitelpunkt den Abstand verringern, damit er gerade einen Überschlag schafft?

Energiesatz am unteren und oberen Scheitelpunkt (II und III):

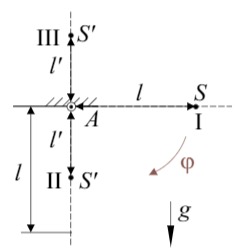
Abbildung

Drehimpulserhaltung:

Eingesetzt in den Energiesatz bei Position folgt mit :

Mit dem verringerten Trägheitsmoment bzgl. folgt:

Werte eingesetzt:

Einzig (physikalisch sinnvolle) reelle Lösung ist der Turner muss seinen Schwerpunkt um näher an die Drehachse heranbringen.

Lösung:

  3. Die Lösung ist , mit den Werten

  5. Einzig (physikalisch sinnvolle) reelle Lösung ist . h. der Turner muss seinen Schwerpunkt um näher an die Drehachse heranbringen.