1 / 18

Aufgabenstellung:

Gegeben sind zwei ideale Schraubenfedern. Ihre Federkonstanten sind und . Welchen Wert hat jeweils die resultierende Federkonstante , wenn die beiden Federn

  1. hintereinander ('Reihenschaltung') bzw.

  2. parallel zueinander gehängt ('Parallelschaltung') werden?
    Die Eigenmassen der beiden Federn sollen dabei vernachlässigt werden.

  3. Wie lauten die Beziehungen für die Schwingungsdauern eines Feder-Masse-Systems für die beiden Konfigurationen, wenn an die Federn jeweils ein Körper der Masse angehängt wird?

Lösungsweg:

Drücke auf "Aufdecken" um dir den ersten Schritt der Lösung anzuzeigen

a) resultierende Federkonstante wenn beide hintereinander ('Reihenschaltung')

Die auf den angehängten Körper (Masse ) wirkende Gewichtskraft bewirkt eine (statische) Verlängerung der beiden Federn. Skizze:

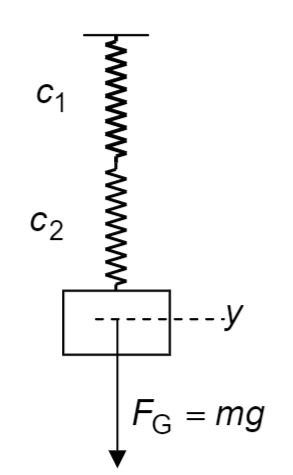
Abbildung

Die wirkende Gewichtskraft ist für beide Federn gleich (die Federn sind idealisierend masselos).

Die Einzelauslenkungen addieren sich zur Gesamtauslenkung.

Mit wird die Auslenkung der Feder '1'

Mit wird die Auslenkung der Feder '2'

Die Gesamtauslenkung der Anordnung ist

Gewichtskraft auf die Gesamtanordnung ist

Koeffizientenvergleich liefert für die resultierende Federkonstante

Merke: Bei einer Reihenschaltung addieren sich die reziproken Federkonstanten der beiden Einzelfedern zur reziproken Federkonstante der Resultierenden.

b) wenn beide parallel zueinander gehängt ('Parallelschaltung')

Die Skizze für die Parallelschaltung ist 'symbolisch' aufzufassen. Denken Sie sich für die folgende Rechnung die beiden Federn in einander gesteckt. Die Auslenkungen sind notwendig für beide Federn gleich. Skizze:

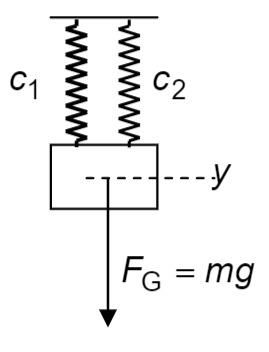
Abbildung

Die beiden Einzelkräfte addieren sich zur Gesamtkraft. Die beiden Einzelkräfte sind

Die Gesamtkraft ist

Die Gewichtskraft auf die Gesamtanordnung

Koeffizientenvergleich liefert für die resultierende Federkonstante

Merke: Bei einer Parallelschaltung addieren sich die Federkonstanten der beiden Einzelfedern zur Federkonstante der Resultierenden.

c) die Beziehungen für die Schwingungsdauern eines Feder-Masse-Systems 

Schwingungsdauern für die Anordnungen der Teilaufgaben (a) und (b) Die Schwingungsdauern ergeben sich mit der jeweils berechneten resultierenden Federkonstanten jeweils zu

Damit gilt für die Reihenschaltung aus (a)

Damit gilt für die Parallelschaltung aus (b)

Lösung:

  1. Bei einer Reihenschaltung addieren sich die reziproken Federkonstanten der beiden Einzelfedern zur reziproken Federkonstante der Resultierenden.

  2. Bei Parallelschaltung addieren sich die Federkonstanten der beiden Einzelfedern zur Federkonstante der Resultierenden.

  3. Reihenschaltung (a)
    Parallelschaltung (b)