Aufgabenstellung:
Die nachstehenden in der Parameterform vorliegenden Funktionen sind in der expliziten kartesischen Form
Um welche Kurven handelt es sich dabei?
Bestimmen Sie den Definitionsbereich und skizzieren Sie den Kurvenverlauf.
Lösungsweg:
Wir lösen die Parametergleichungen nach
Skizze:
Die letzte Gleichung beschreibt eine Ellipse mit dem Mittelpunkt
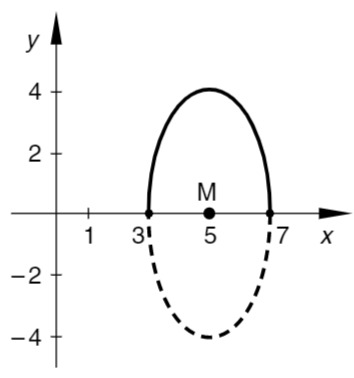
Die Ellipse wird in expliziter Form wie folgt beschrieben (Ellipsengleichung nach
Definitionsbereich
Lösung:
Skizze siehe Musterlösung