Aufgabenstellung:
Durch ungestörte Überlagerung der beiden zueinander senkrechten Schwingungen mit den Gleichungen
entsteht eine sog. Lissajous-Figur
Beschreiben Sie die Bahnkurve in kartesischen Koordinaten für
,
und skizzieren Sie die Kurven.
Lösungsweg:
a) Im Falle
Die Parametergleichungen lauten für
Unter Verwendung der trigonometrischen Formeln
Die
Wir erhalten somit zwei (ungerade) Funktionen, die durch Spiegelung an der
Skizze
Wertetabelle (
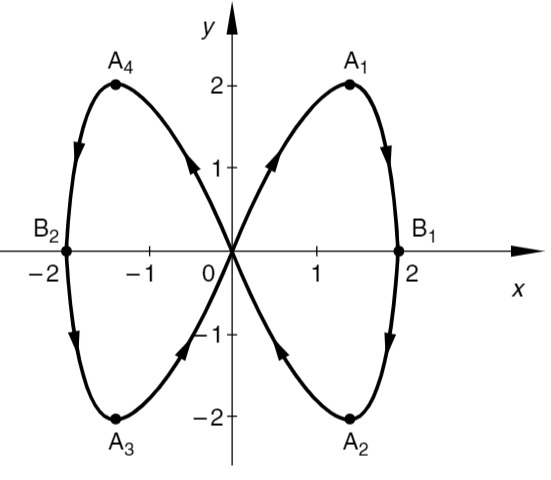
Die geschlossene Kurve wird dabei innerhalb der Periode
Startpunkt:
b) Im Falle von
Parametergleichungen für
Die
Aus der
Skizze
Die (periodische) Bewegung verläuft längs einer Parabel zwischen den Punkten
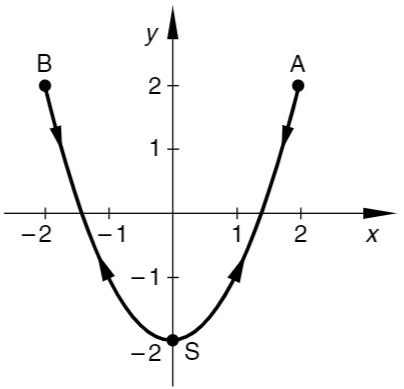
Die geschlossene Kurve wird innerhalb einer Periode
Lösung:
Skizzen siehe Musterlösung