Aufgabenstellung:
Ein Elektron mit der Masse

a) Mit welcher Geschwindigkeit
b) Welche Bedingung muss erfüllt sein, damit das Elektron das Magnetfeld auf der rechten Seite verlässt?
c) Unter welchem Winkel
d) Wie lange benötigt das Elektron von der linken Kondensatorplatte bis zum Austritt aus dem Magnetfeld?
Hinweis:
Feldstreuungen sind als vernachlässigbar anzusehen. Außerdem wird angenommen, dass die auftretenden Geschwindigkeiten so gering sind, dass keine relativistischen Effekte berücksichtigt werden müssen.
Lösungsweg:
a) Geschwindigkeit
Für die beim Bewegen einer Ladung zugeführte Energie
Die auf das Teilchen wirkende Kraft
Setzt man Gleichung (1) in Gleichung (2) ein, so steht unter dem Integral ein Spatprodukt.
Die Faktoren eines Spatproduktes dürfen zyklisch vertauscht werden, ohne dass sich das Vorzeichen ändert.
Da
Daraus folgt:
Anstatt die Geschwindigkeit des Elektrons beim Verlassen des Plattenkondensators direkt zu berechnen, ist es bequemer, zuerst den Energiezuwachs und erst dann die Geschwindigkeit zu bestimmen. Die Kraft, die auf das Elektron im Kondensator ausgeübt wird, ist gleich
Setzt man die Kraft in Gleichung (1) ein, erhält man
Nach dem Durchlaufen des elektrischen Feldes, hat sich die kinetische Energie des Elektrons um
Damit gilt
Um die gesuchte Geschwindigkeit zu erhalten, muss (5) nur noch umgestellt werden.
b) Bedingung ?
Die auf das Elektron im Magnetfeld wirkenden Kräfte wirken stets senkrecht zum Geschwindigkeitsvektor und der Feldstärke. Dies führt dazu, dass das Teilchen eine Kreisbahn beschreibt.
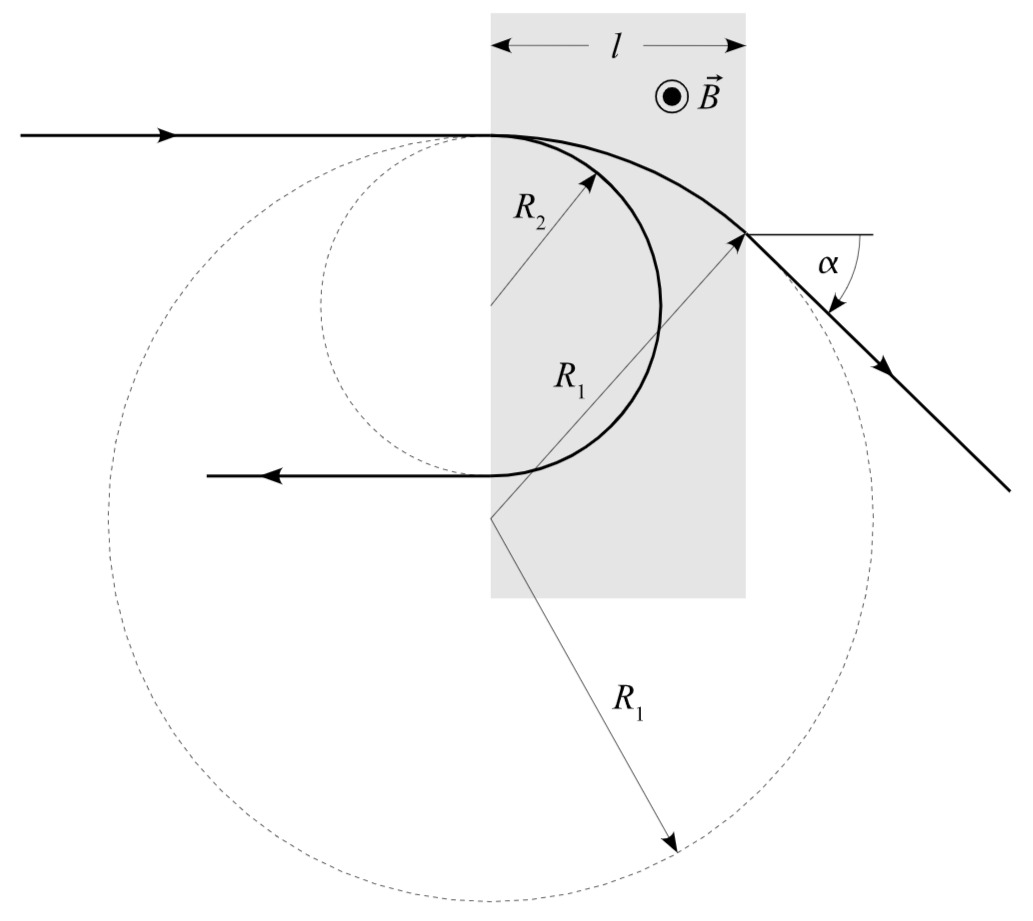
Wenn der Radius
Auf das Elektron wirkt zum einen die durch das Magnetfeld bewirkte Zentripetalkraft und zum anderen eine Zentrifugalkraft
und damit den Bahnradius
Damit das Elektron auf der rechten Seite des Magnetfeldes austritt, muss daher unter Berücksichtigung von Gleichung
Zentrifugalkraft
c) Winkel
Aus der Abbildung (Siehe Aufgabenteil b) kann man direkt den Zusammenhang zwischen dem Bahnradius
d) Zeit bis zum Austritt
Die Gesamtflugzeit
(1)
(2)
(3)
zu (1):
Die Berechnung der Zeit
Neben Gleichung (7) gilt für das elektrische Feld eines Plattenkondensators die Beziehung
und für die Wegstrecke
Unter Ausnutzung der Gleichung
Umstellen nach
Zum Zeitpunkt
zu (2):
Die Endgeschwindigkeit des Elektrons beim Austritt aus dem Kondensator erhält man aus Gleichung (6). Mit ihr lässt sich die Zeit
zu (3):
Die Länge des von dem Elektron im Magnetfeld zurückgelegten Bogens im Magnetfeld ist gleich
Addiert man alle drei Zeiten, so erhält man die gesamte Flugzeit des Elektrons.
Lösung:
a)
b)
c)
d)