Aufgabenstellung:
Zwei Spulen sind auf einen gemeinsamen Eisenkern mit den unten angegebenen Abmessungen
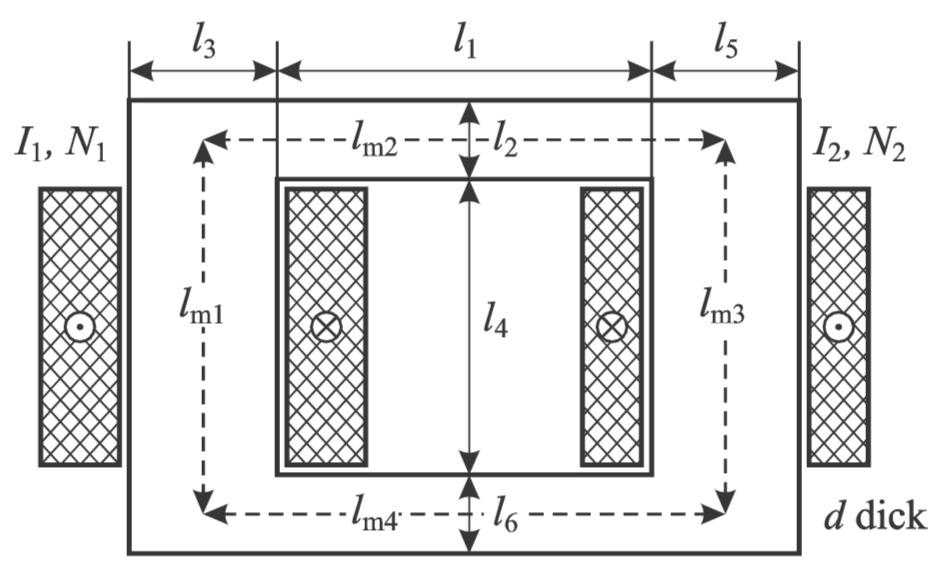
a) Berechnen Sie allgemein die vier gestrichelt eingezeichneten mittleren Feldlinienlängen
b) Zeichnen Sie das magnetische Ersatzschaltbild der Anordnung und geben Sie allgemein jeweils die Größen
c) Die magnetische Flussdichte
d) Bestimmen Sie die magnetischen Feldstärken und Flussdichten in den vier Abschnitten wenn
Lösungsweg:
Ansatz
- Aufstellen des magnetischen Ersatzschaltbildes
- Bestimmung der mittleren Feldlinienlängen
- Bestimmung des magn. Flusses
- Bestimmung der magn. Flussdichte
b) Magnetisches Ersatzschaltbild
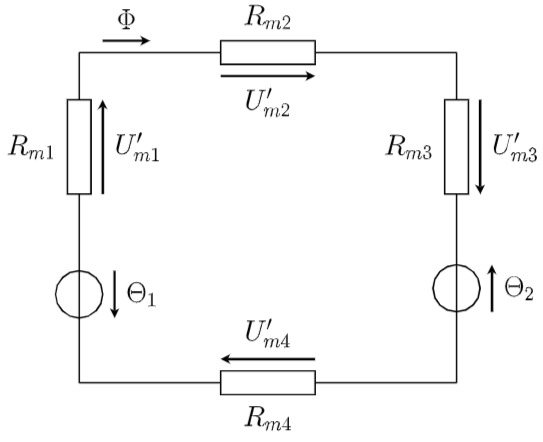
Für die angegebene Anordnung ergibt sich das Ersatzschaltbild des magnetischen Kreises im Bild.
Für den magnetischen Widerstand
und für die magnetische Spannung
Die Größen des Ersatzschaltbildes bestimmen sich wie folgt:
a) Bestimmung der mittleren Feldlinienlängen
c) Bestimmung des magn. Flusses
Allgemein gilt für den magnetischen Fluss
Um dieses Integral lösen zu können, muss die Querschnittsfäche A des Eisenkerns bestimmt werden. Dazu muss nun das Flächenelement
In x-Richtung (hier ist das die horizontale Richtung) muss beispielsweise integriert werden von
und in
Für die rechte Seite gilt entsprechendes, oben und unten sind die Breiten
d) Berechnung der magn. Flussdichten und Feldstärken
Es gilt hier wieder das Durchflutungsgesetz
Unter der Annahme, das
Wendet man dieses auf den Eisenkern an, ergeben sich vier Teilabschnitte, und damit vier Feldstärken
Hierzu vergleiche man die Gleichung aus dem magnetischen Ersatzschaldbild:
Unter der Ausnutzung der Symmetrien des Eisenkerns ist
Mit den gegebenen Werten ergibt sich
Die gesuchte Flussdichte kann durch die folgend Beziehung bestimmt werden:
Lösung:
siehe Lösungsweg