6 / 7

Aufgabenstellung:

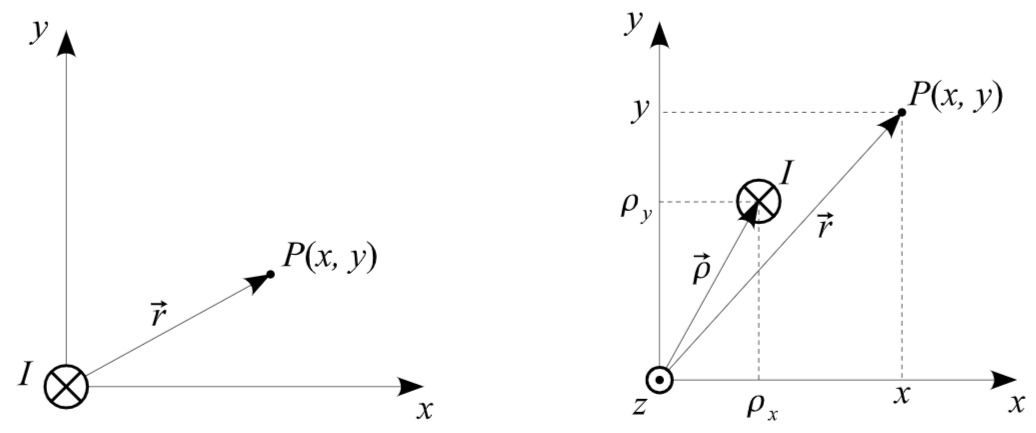
Ein unendlich langer, gerader Leiter mit kreisförmigem Querschnitt wird von dem Strom durchflossen. Der Leiter liegt im Nullpunkt der -Ebene eines kartesischen Koordinatensystems und verläuft parallel zur -Achse. Die Zählrichtung des Stromes weist in der linken Abbildung in die Zeichenebene hinein, also in -Richtung.

Abbildung

Abbildung 1

a) Bestimmen Sie die magnetische Feldstärke an einem beliebigen aber festen Punkt außerhalb des Leiters. Stellen Sie den Vektor der magnetischen Feldstärke als Summe seiner kartesischen Komponenten dar.

Der Leiter steht weiterhin senkrecht auf der -Ebene des kartesischen Koordinatensystems. Der Leitermittelpunkt wird nun aber gegenüber dem Koordinatenursprung um verschoben (Abbildung rechts).

b) Bestimmen Sie die magnetische Feldstärke im Punkt . Stellen Sie den Vektor der magnetischen Feldstärke als Summe seiner kartesischen Komponenten dar.

Lösungsweg:

Drücke auf "Aufdecken" um dir den ersten Schritt der Lösung anzuzeigen

a) magnetische Feldstärke

Ein gerader vom Strom durchflossener Leiter mit kreisförmigem Querschnitt erzeugt außerhalb des Leiters im Abstand von seinem Mittelpunkt eine magnetische Feldstärke, deren Feldlinien konzentrische Kreise um den Leitermittelpunkt bilden. Die Richtung der Feldlinien ist mit der Stromzählrichtung durch ein Rechtssystem verknüpft.

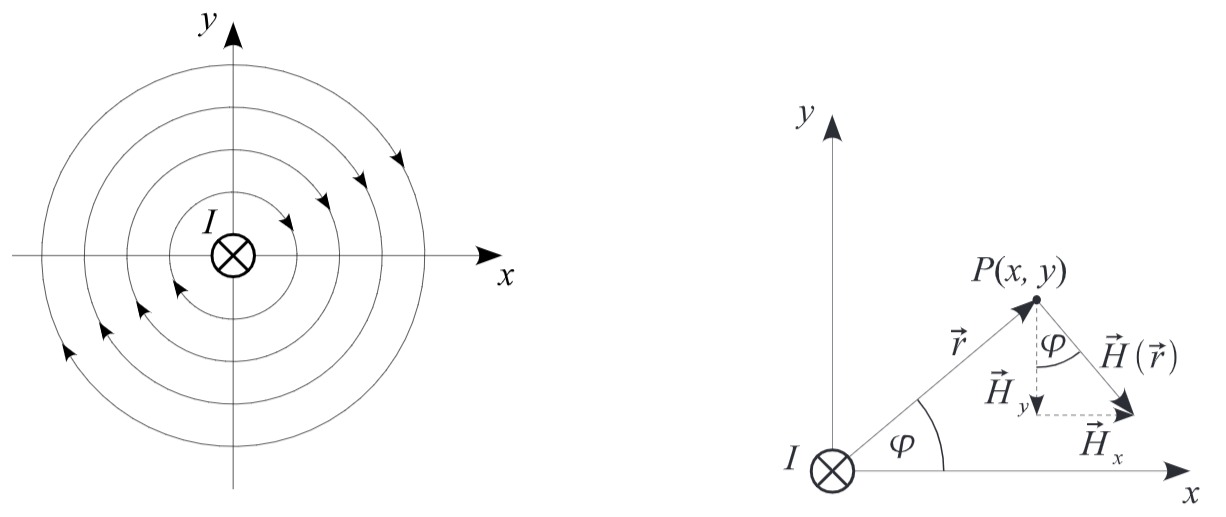
Abbildung

Abbildung 2

Hinweis:
Ein Rechtssystem ist durch das Kreuzprodukt seiner Einheitsvektoren definiert. So gilt zum Beispiel (für Zylinderkoordinaten):

Das Ergebnis des Kreuzprodukts ist ein Vektor, der senkrecht auf der von den beiden anderen Vektoren aufgespannten Ebene steht. Das Vorzeichen des Ergebnisses hängt von der Reihenfolge der Produktterme ab. Das Produkt ist nicht kommutativ. Bildet man das Kreuzprodukt in der angegebenen Reihenfolge, erhält der Ergebnisvektor ein positives Vorzeichen. Kehrt man dagegen die Reihenfolge um, erhält der Ergebnisvektor ein negatives Vorzeichen.

Kommen wir jetzt zurück zu dem Zusammenhang zwischen der Richtung des Stroms in dem geraden Leiter und der Richtung des Feldstärkevektors.

  • Man erhält die Stromrichtung aus dem Feldstärkevektor, indem man das Kreuzprodukt aus dem Einheitsradiusvektor und dem Einheitsvektor der Feldstärke bildet.

  • Man erhält die Richtung des Feldstärkevektors aus der Stromrichtung, indem man das Kreuzprodukt aus der Stromrichtung und dem Einheitsradiusvektor bildet.

Wendet man diese Regel auf die Anordnung in Abbildung an, so erhält man

Kombiniert man die Gleichungen (1) und (2), erhält man den magnetischen Feldstärkevektor

Nun ist allerdings in der Aufgabenstellung gefordert, dass der Feldstärkevektor als Summe seiner kartesischen Komponenten dargestellt wird. Dazu muss der Einheitsvektor in die kartesischen Komponenten zerlegt werden.

Möglichkeit 1:

Wie man aus Abbildung (1) ablesen kann, gilt für die Vektorzerlegung

Setzt man Gleichung (4) in (3) ein, erhält man das Ergebnis

Um die magnetische Feldstärke als Funktion der kartesischen Koordinaten und anzugeben, müssen die Gröfen und in Gleichung durch und ausgedrückt werden.

Setzt man die Gleichungen (6) bis (8) in (5) ein, erhält man das gewünschte Resultat.

Dieses Vorgehen setzt jedoch voraus, dass Gleichung (5) bereits als Zwischenergebnis vorliegt.

Möglichkeit 2

Mit Hilfe des Kreuzproduktes kann man den Einheitsvektor auch durch die Einheitsvektoren und darstellen.

Setzt man diese Beziehung in Gleichung (3) ein, erhält man

Anschließend wird Gleichung (9) noch mit dem Betrag des Abstandsvektors erweitert.

Mit dieser Darstellungsform tritt das Problem der Vektorzerlegung von gar nicht erst auf. Der Abstandsvektor kann völlig problemlos in seine kartesischen Komponenten zerlegt werden. Ersetzt man jetzt in Gleichung (10) den Abstandsvektor durch seine kartesischen Komponenten, führt dies auf

Zuletzt muss noch das Kreuzprodukt mit gebildet werden.

Damit hat man auf einem anderen Lösungsweg das gleiche Ergebnis wie in Gleichung (11) erzielt.

b) magnetische Feldstärke 

Der Leitermittelpunkt liegt nun nicht mehr im Koordinatenursprung. Die Feldlinien der magnetischen Feldstärke bilden auch hier konzentrische Kreise um den Leitermittelpunkt, aber nicht um den Koordinatenursprung.

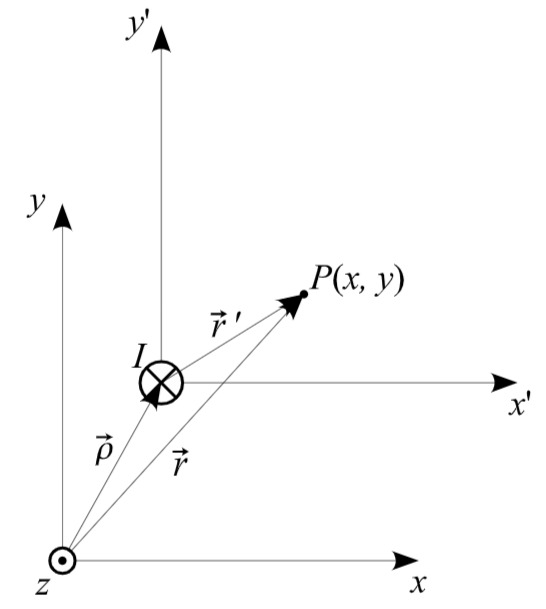
Abbildung

Abbildung 3

Um dennoch die Ergebnisse aus a) verwenden zu können, wird ein Hilfskoordinatensystem eingeführt. Die Achsen dieses Systems sind mit und bezeichnet. Der Koordinatenursprung des Hilfssystems liegt im Leitermittelpunkt. Der Abstandsvektor zwischen dem Leitermittelpunkt und dem Punkt , in welchem das magnetische Feld bestimmt werden soll, wird mit bezeichnet. Damit kann die Formel für die magnetische Feldstärke aus a) übernommen werden. Allerdings sind dabei die Koordinaten des Hilfssystems zu verwenden.

Die gesuchte Feldstärke soll jedoch nicht in den Koordinaten des Hilfskoordinatensystems sondern in denen des gegebenen Systems ausgedrückt werden. Dazu muss durch die gegebenen Größen ersetzt werden. Aus Abbildung lässt sich die folgende Vektorzerlegung ablesen

ersetzt man nun in Gleichung (12) durch diesen Ausdruck, so erhält man

Nun müssen die Abstandsvektoren und in ihre kartesische Komponenten zerlegt werden.

Im letzten Schritt muss noch das Vektorprodukt ausgeführt werden.

Lösung:

a)

b)