Aufgabenstellung:
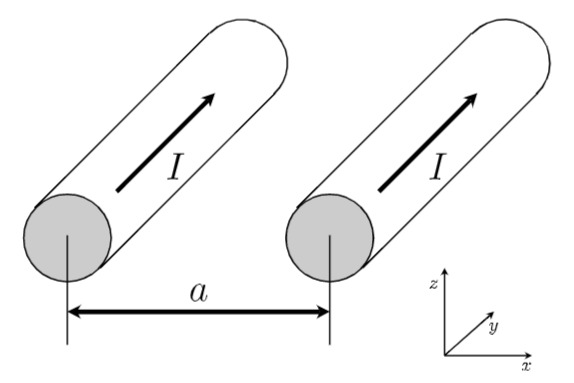
Gegeben ist eine lange Doppelleitung mit
a) Für einen Strom
b) Leiten Sie allgemein den Betrag der Feldstärke
c) Überlagern Sie die einzelnen Feldstärken für den Sonderfall
d) Warum kann man die Gesamtfeldstärke aus den Beträgen der Einzelfeldstärken für die Leiter nur in bestimmten Sonderfällen einfach bestimmen?
e) Zeichnen Sie den Betrag der Feldstärke auf der
f) Im Fall eines Kurzschlusses ergebe sich ein Kurzschlussstrom
Lösungsweg:
Erklärung des Problems
- Kraftwirkung: LORENTZkraft
- Jeder Leiter hat ein eigenes Feld
- Überlagerung der Felder
- Kraftwirkung auf die Leiter
Vorgehen in der Lösung:
1. (Allgemeine) Bestimmung des Feldes eines Leiters
2. Koordinatenverschiebung
3. Überlagerung der einzelnen Felder
4. Zeichnen des Feldes entlang der
5. Berechnen der Kraft auf einen Leiter
6. Ausnutzen der Symmetrie
7. Überlagerung der Kräfte
Aufgabenteil a)
Zunächst die Skizze für einen einfachen Leiter:
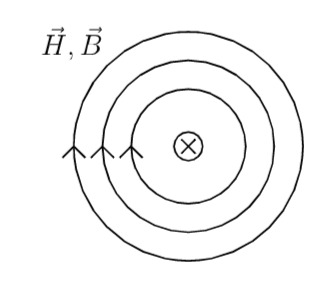
Die Überlagerung der beiden Felder ergibt:
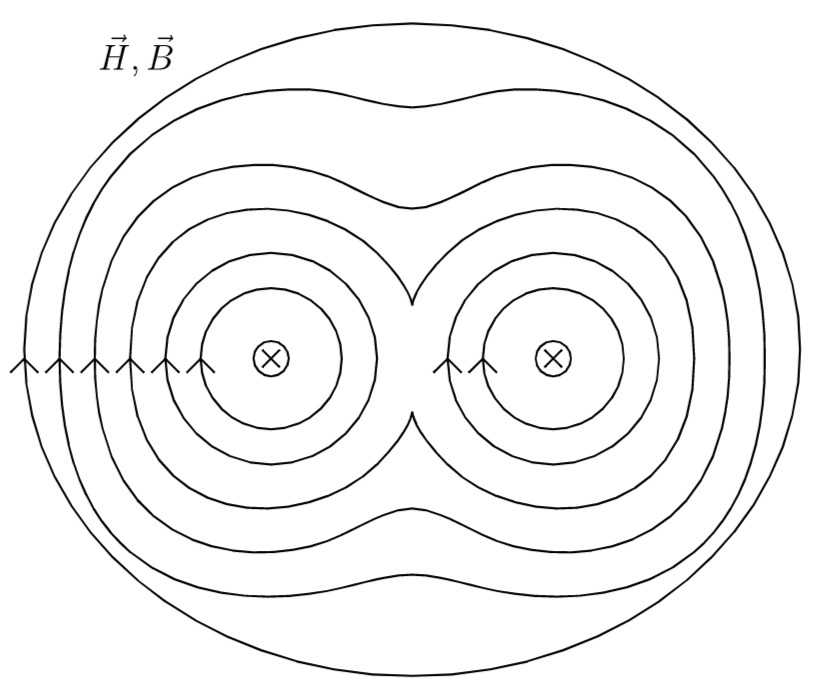
Die Felder werden zwischen den beiden Leitern geschwächt, da hier die Feldlinien "entgegengesetzt " verlaufen.
Aufgabenteil b)
Die magnetische Feldstärke außerhalb des Leiters wird nach dem Durchflutungssatz berechnet. Es gilt:
wobei
Für einen Leiter, der im Ursprung sitzt ergibt sich daher folgende Gleichung für den Betrag der Feldstärke:
Beide Leiter liegen jedoch prinzipiell irgendwo im Koordinatensystem. Wir drücken also beide Gleichungen mit Indizes aus, damit sie später einfach überlagert werden können. Dabei braucht man nur die Variablen zu indizieren, die bei beiden unterschiedlich sind:
Nun müssen ein Bezugspunkt sowie eine Richtung der Achsen für das Koordinatensystem gewählt werden.
Ergänzung: Richtung der Achsen
Hierbei ist es prinzipiell egal, wo der Ursprung liegt bzw. in welche Richtung die Achsen zeigen. Hier kann z. B. zur Verdeutlichung ruhig auch einmal eine vollkommen unsinnige Koordinatensystem-Wahl gezeigt werden, wie im Bild zu sehen ist. Auf die Probleme mit solchen Festlegungen für das Koordinatensystem kurz eingehen. Folgende Punkte können erwähnt werden:
- Berechnung der einzelnen Transformationsvorschriften schwierig, dadurch schleichen sich Fehler ein
- fehlende Symmetrie vermindert die Fehlerauffälligkeit
- manchmal fallen durch geschickte Symmetrierung Terme weg, die die Rechnung erleichtern. Das ist hier sehr oft nicht der Fall.

Damit dürfte die Wahl der Richtung klar sein.
Für den Urspung bieten sich sinnvollerweise drei Möglichkeiten an, die gleichwertig sind:
1. Ursprung im linken Leiter: Dabei braucht nur die Gleichung für die Feldstärke des rechten Leiters angepasst zu werden,
2. Ursprung im rechten Leiter: Dabei braucht nur die Gleichung für die Feldstärke des linken Leiters angepasst zu werden und
3. Ursprung in der Mitte zwischen beiden Leitern. Hierbei müssen zwar beide Gleichungen angepasst werden, die Gleichung sieht aber symmetrisch aus.
Man kann natürlich auch den Ursprung in
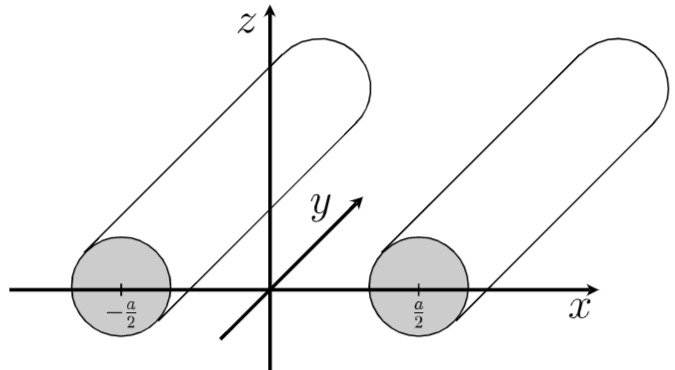
Da nun beide Leiter bei
Nun ist noch jeweils das
Wir erhalten daher:
und
Aufgabenteil
Nun erfolgt die Überlagerung der beiden Felder für den Spezialfall
Durch
Die magnetische Flussdichte ergibt sich über den einfachen Zusammenhang
Dementsprechend gibt es andere Werte, also eine andere Skalierung der Ordinate.
Aufgabenteil d)
Die einfache Überlagerung der Beträge der Feldstärken funktioniert nur dann einfach, wenn die Vektoren gleich- oder genau entgegengesetzt gerichtet sind. Dieses ist in diesem Fall nur entlang der
Aufgabenteil
Die Zeichnung für die Magnetische Feldstärke entlang der x-Achse sieht wie folgt aus

Aufgabenteil
Die Kraftwirkung auf die Leiter wird durch die Lorentzkraft verursacht.
Magnetsiche Flussdichte im jeweils anderen Leiter:
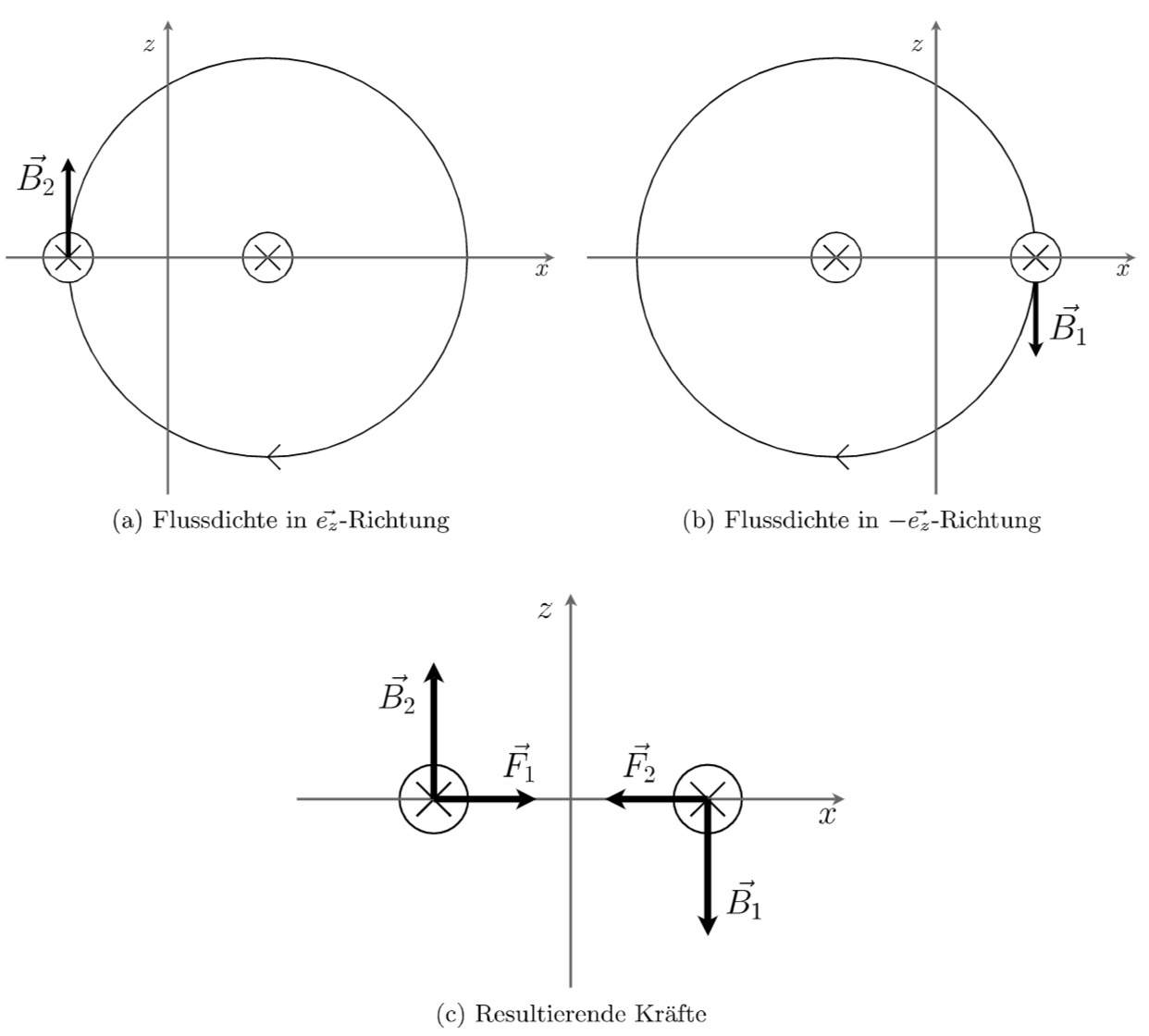
Die Abbildung zeigt die parallel zur
genutzt. Das Integral folgt aus der Überlegung, dass sich die Kraft aus einzelnen Kraftkomponenten zusammensetzt. Jede dieser Komponenten muss nun über das Kreuzprodukt berechnet und integriert werden.
Wir berechnen die Kraft zunächst für den linken Leiter:
Für den rechten Leiter ergibt sich quasi dasselbe:
Beide Resultate unterscheiden sich lediglich im Vorzeichen. Daher kann man zunächst den Betrag der Kraft berechnen. Dieser ist gegeben durch:
Die Kraft in
Lösung:
siehe Lösungsweg