Aufgabenstellung:
In einem langen Draht fließt der zeitlich konstante Strom
a) Berechnen Sie mit dem Durchflutungsgesetz den Feldstärkeverlauf im Inneren des Ringkerns abhängig vom Radius in allgemeiner Form.
b) Bestimmen Sie den magnetischen Fluss
c) Bestimmen Sie den magnetischen Fluss
Lösungsweg:
Aufgabenteil a)
Gesucht: Die magnetische Feldstärke im Ringkern
Gegeben:
Ansatz:
Das Durchflutungsgesetz in allgemeiner Form lautet
Betrachtet wird der Verlauf der Feldlinien im Ringkern
Linienelement und Feldline
Die Parametrisierung des Ringkerns ergibt
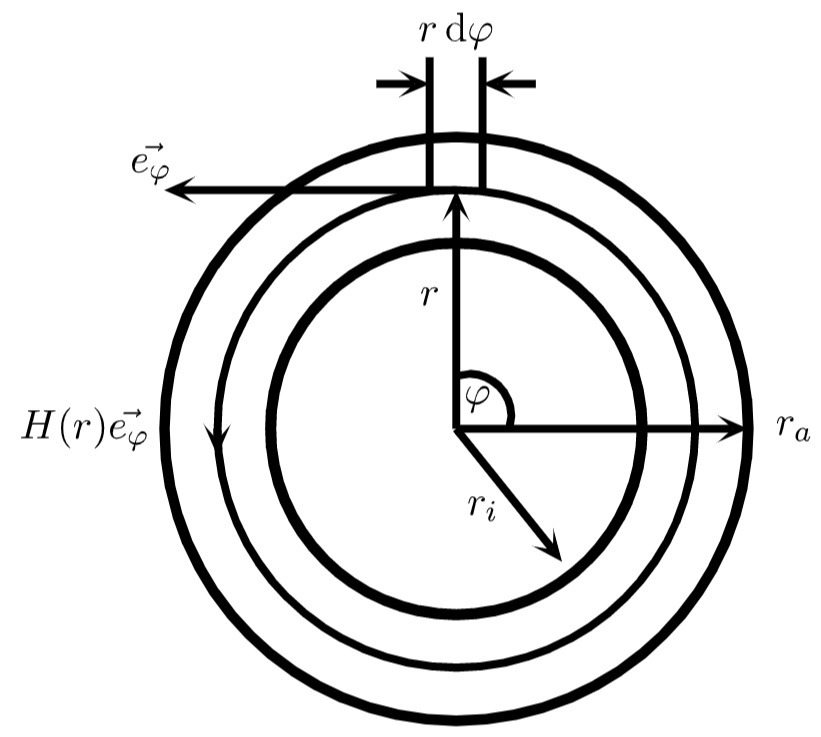
Aufgrund der Aufgabenstellung kann das Durchflutungsgesetz geschrieben werden als
die magnetische Feldstärke im Ringkern ist dann
Aufgabenteil b)
Gesucht: Magnetischer Fluss
Gegeben:
Ansatz:
Allgemein gilt für den magnetischen Fluss
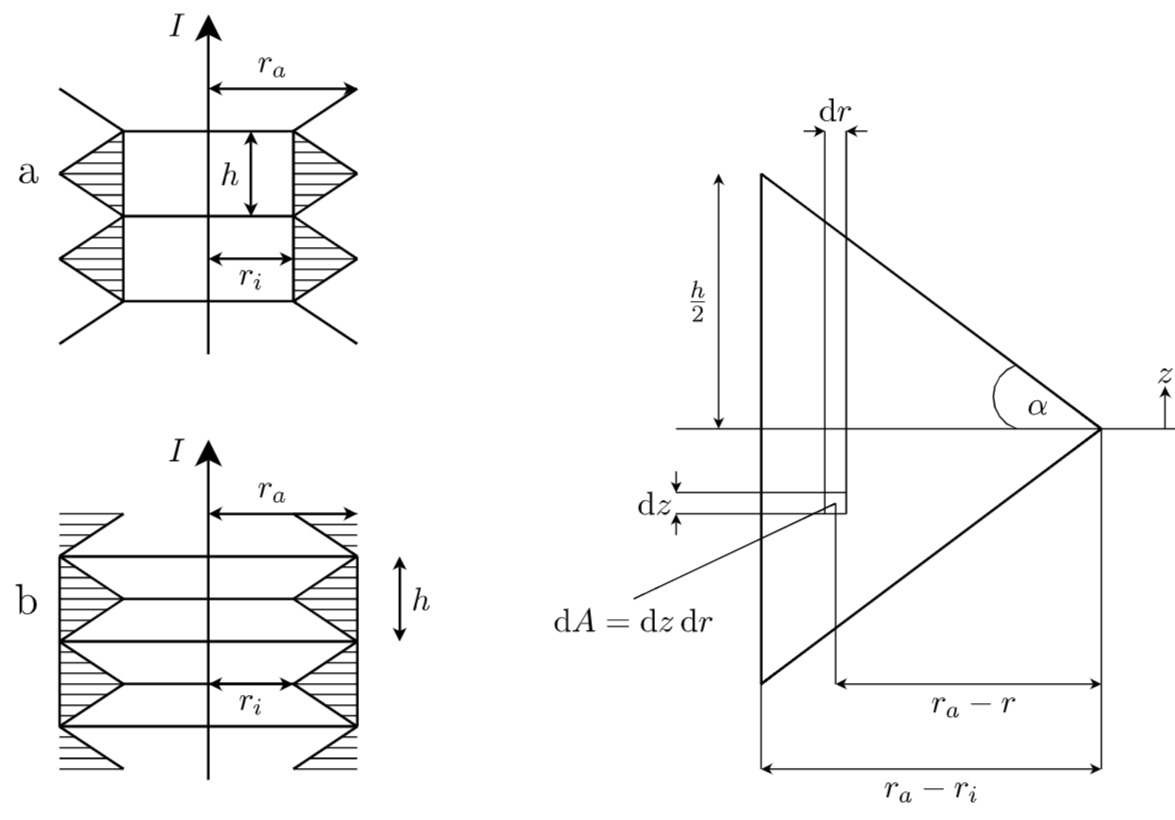
Um das Integral lösen zu können, muss die Querschnittsfäche
In
wobei

Mit Hilfe der Tangensbeziehungen
kann die Abhängigkeit der Höhe
Damit ergibt sich
Mit den gegebenen Werten wird
Aufgabenteil
Gesucht: Magnetischer Fluss
Ansatz:
siehe Fall a.
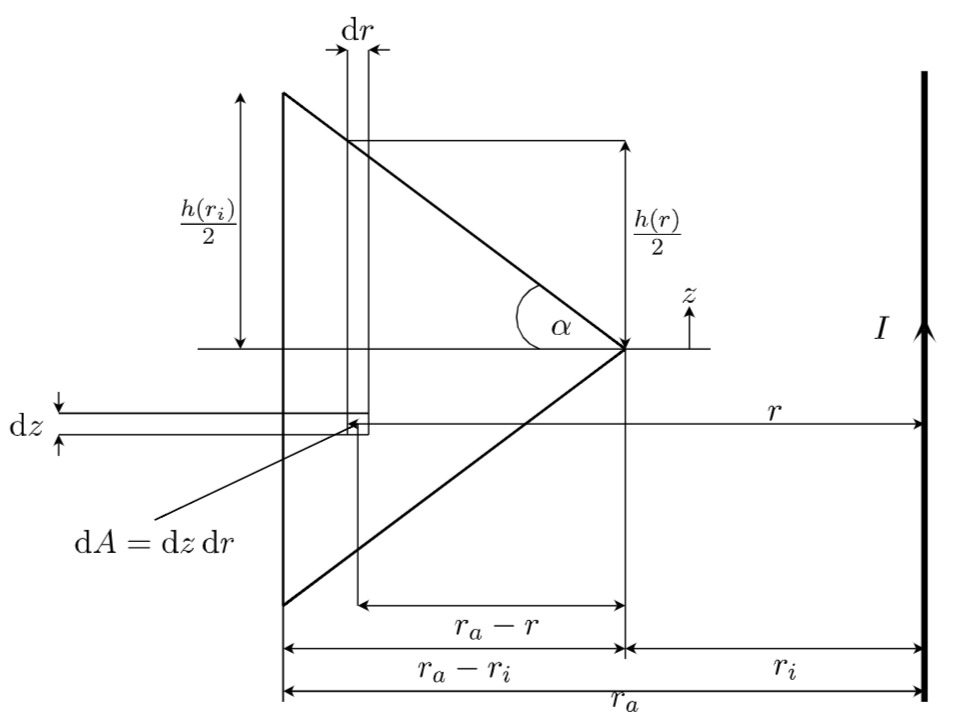
Mit Hilfe der Tangensbeziehungen
kann die Abhängigkeit der Höhe
Damit ergibt sich
Mit den gegebenen Werten wird
Lösung:
siehe Lösungsweg