Aufgabenstellung:
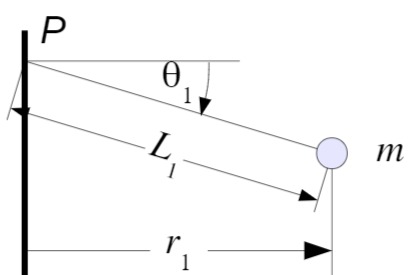 Am Ende des masselosen Seils der Länge
Am Ende des masselosen Seils der Länge
- Wie groß sind der Winkel
der Radius , die Seilkraft und die Winkelgeschwindigkeit - Nun wird das Seil auf die Länge
verkürzt, so dass sich die Masse auf einer Kreisbahn mit Radius um den Pfosten bewegt. Wie groß sind die Geschwindigkeit die Winkelgeschwindigkeit der Winkel die Länge und die Seilkraft ?
Gegeben:
Lösungsweg:
a) Mit einer Seillänge
An der freigeschnittenen Masse greifen die Seilkraft
Lageplan

Kräfteplan
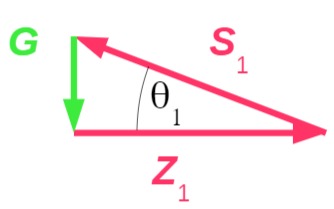
Der Kräfteplan zeigt:
Mit
Die zweite Lösung scheidet aus, da der Wert des Sinus zwischen -1 und 1 liegen muss.
Zahlenwert:
Der Radius
Für die Seilkraft gilt:
Schließlich berechnet sich die Winkelgeschwindigkeit zu
b) Mit einer Seillänge
Die Wirkungslinie der Kraft, die zur Verkürzung des Seils nötig ist, geht durch die Drehachse. Ihr Moment um die Drehachse ist daher null.
Damit bleibt der Drall der Masse um die Drehachse konstant:
Daraus folgt für die Geschwindigkeit
Und weiter für die Winkelgeschwindigkeit
Für die Zentrifugalkraft
Daraus folgt für den Winkel
Aus
Die Seilkraft berechnet sich wie oben zu
Zahlenwerte: