14 / 15

Aufgabenstellung:

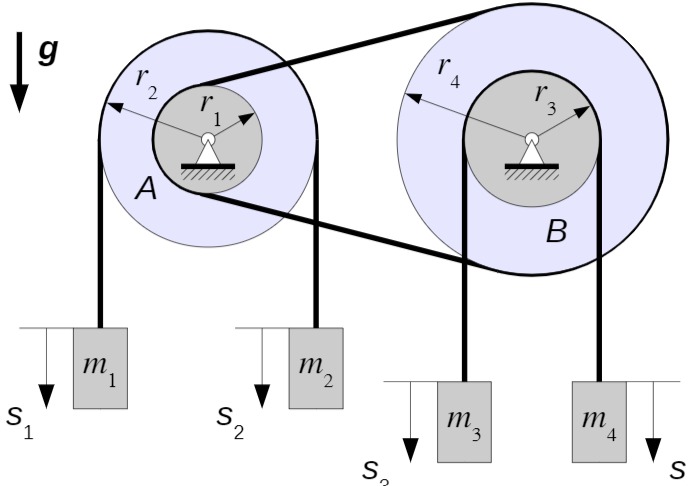AbbildungDie beiden Rollen und sind reibungsfrei gelenkig gelagert und durch einen dehnstarren Riemen verbunden, der auf den Rollen haftet

Über den äußeren Umfang der Rolle verläuft ein dehnstarres Seil, an dem die beiden Massen und befestigt sind.

Über den inneren Umfang der Rolle verläuft ein dehnstarres Seil, an dem die Massen und befestigt sind.
Die Rollen, die Seile und der Riemen sind masselos.

 

  1. Ermitteln Sie mit Hilfe des Energieerhaltungssatzes die Geschwindigkeiten und der Massen in Abhängigkeit vom zurückgelegten Weg der jeweiligen Masse, wenn das System aus der Ruhe losgelassen wird.
  2. Ermitteln Sie die Beschleunigungen und der Massen.
    Zahlenwerte:

Lösungsweg:

Drücke auf "Aufdecken" um dir den ersten Schritt der Lösung anzuzeigen

a) Geschwindigkeiten

Energien

Die einzige äußere Kraft, die am System angreift, ist die Gewichtskraft.
Als Bezugsniveau für die Lageenergie werden die jeweiligen Ruhelagen gewählt. Dann gilt für die Energien:

Kinematische Beziehungen

Als Hilfsgrößen werden die Winke und eingeführt, die die Drehung der Rollen beschreiben:

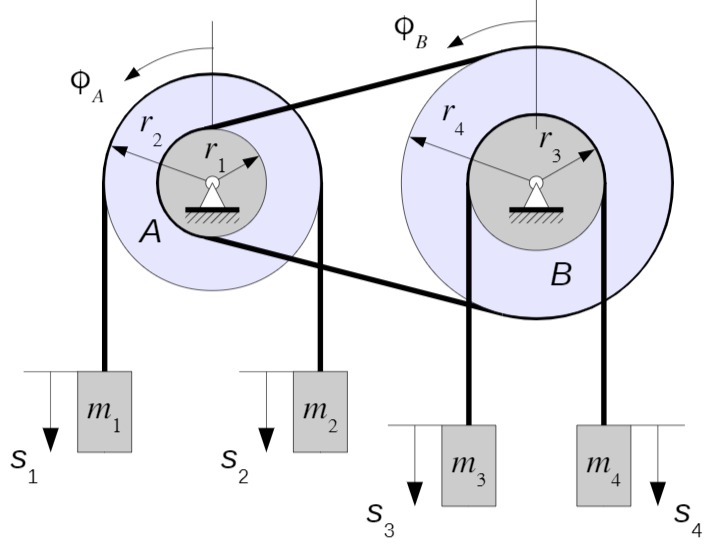
Abbildung

Es gilt:

Für die Geschwindigkeiten folgt:

Energieerhaltungssatz

Mit den kinematischen Beziehungen folgt:

Daraus folgt für die Geschwindigkeit :

Die übrigen Geschwindigkeiten können mit den kinematischen Beziehungen ermittelt werden:

Mit den gegebenen Zahlenwerten folgt:

Damit der Ausdruck unter der Wurzel positiv ist, muss positiv sein. Die Masse bewegt sich daher nach unten, und inre Geschwindigkeit ist positiv:

Die Auslenkung ist negativ, und für die Geschwindigkeit gilt:

Entsprechend folgt für die Geschwindigkeiten und :

b) Beschleunigungen

Lösung: