11 / 12

Aufgabenstellung:

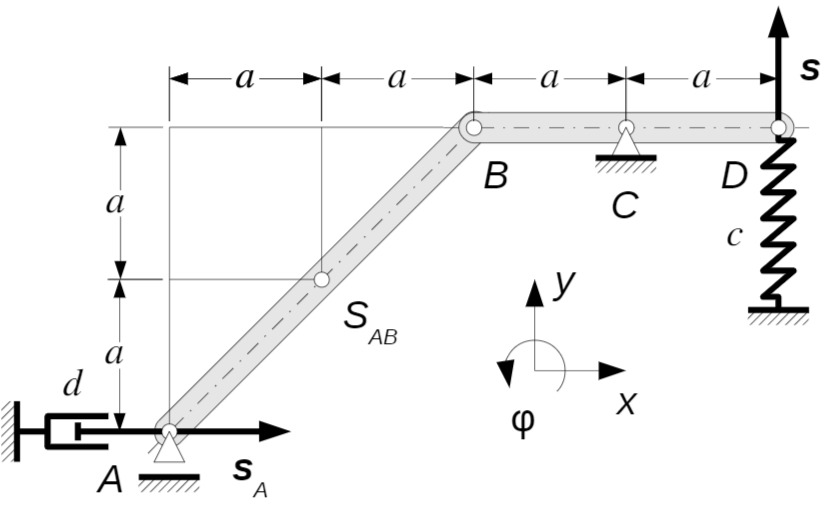AbbildungDas abgebildete System besteht aus den dünnen homogenen Stangen (Masse ) und (Masse ), die im Punkt reibungsfrei ge lenkig miteinander verbunden sind. Die Stange wird im Punkt durch ein Loslager und die Stange im Punkt durch ein Festlager gehalten. Im Punkt ist ein linearer Dämpfer mit der Dämpferkonstanten und im Punkt eine lineare Feder mit der Federkonstanten angeschlossen.

Die Auslenkungen dürfen als klein angenommen werden

  1. Berechnen Sie die Massenträgheitsmomente und der Stangen bzw.
  2. Ermitteln Sie die Winkelgeschwindigkeiten und der Stangen bzw. die Geschwindigkeit von Punkt sowie die Geschwindigkeiten und des Schwerpunkts in Abhängigkeit von der Geschwindigkeit von Punkt
  3. Stellen Sie alle kinetischen Gleichungen auf, die zum Aufstellen der Schwingungsgleichung benötigt werden. Die kinematischen Beziehungen aus b) sollen noch nicht eingesetzt werden
  4. Stellen Sie die Schwingungsgleichung auf und ermitteln Sie die Abklingkonstante und die Eigenkreisfrequenz .

Gegeben:


Lösungsweg:

Drücke auf "Aufdecken" um dir den ersten Schritt der Lösung anzuzeigen

a) Massenträgheitsmomente

b) Kinematik

Abbildung

Stange :

Stange

Alternative Lösung ohne Momentanpol (Stange :

Als Bezugspunkt für die Kinematik von Stab wird Punkt gewählt.

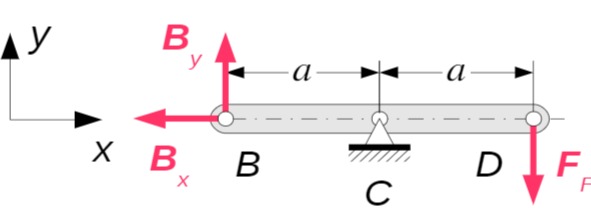
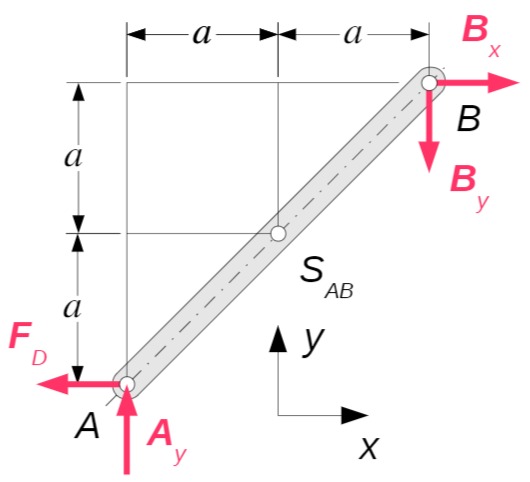
c) Kinetik

Stange

Abbildung

Lineare Feder:

Stange

Abbildung

Linearer Dämpfer:

d) Schwingungsgleichung

Zuerst werden die Gelenkkräfte eliminiert:

(1) und (2)

(3) und (6)

(4)

Einsetzen der Kräfte in (5) ergibt:

Mit den Beziehungen für die Massen und die Massenträgheitsmomente folgt:

Einsetzen der kinematischen Beziehungen ergibt:

Daraus folgt die Schwingungsgleichung:

Aus der Schwingungsgleichung kann abgelesen werden:

Lösung:

  3. Siehe Lösungsweg.