Aufgabenstellung:
Die Masse
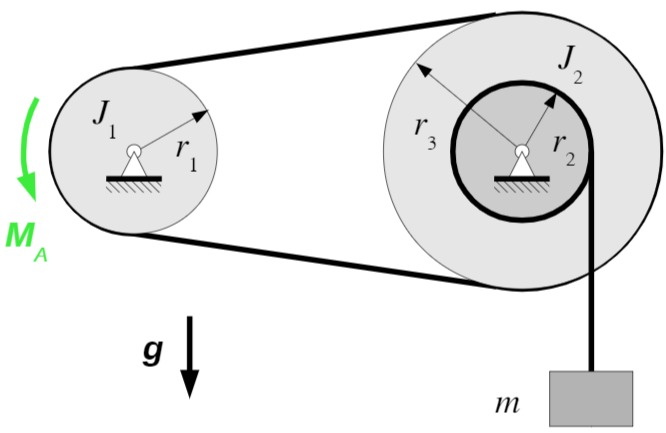
- Wie hängen die Winkelgeschwindigkeiten
und der beiden Rollen von der Geschwindigkeit ab, mit der die Masse angehoben wird? - Welche Beziehung besteht zwischen der Geschwindigkeit
und dem Weg um den die Masse angehoben wurde, wenn die Masse anfangs in Ruhe ist? - Welchen Wert hat das kleinste Antriebsmoment
, das zum Heben der Last erforderlich ist? - Welche Beschleunigung
erfährt die Masse für
Gegeben:
Lösungsweg:
a) Kinematische Beziehungen

Riemen und Seil sind dehnstarr. Daher gilt:
b) Geschwindigkeit in Abhängigkeit vom Weg
An dem Gesamtsystem greift die Gewichtskraft und das Antriebsmoment an. Die Aufgabe wird mit dem Arbeitssatz gelöst.
- Zustand
: Ruhezustand - Zustand
Die Masse hat den Weg nach oben zurückgelegt. - Das Nullniveau für die Lageenergie der Masse wird in die Ruhelage gelegt.
Kinetische Energien:
Lageenergien:
Arbeit des Antriebsmoments:
Wird der Winkel aus der Ruhelage gemessen, dann gilt:
Aus
Damit gilt:
Der Arbeitssatz lautet:
Einsetzen ergibt:
Daraus folgt die gesuchte Größe:
c) Kleinstes Antriebsmoment
Für das kleinste Antriebsmoment ist die Beschleunigung der Masse null. Bei ortsabhängiger Geschwindigkeit gilt für die Beschleunigung:
Aus
Zahlenwert:
d) Beschleunigung
Mit
Zahlenwert: