Aufgabenstellung:
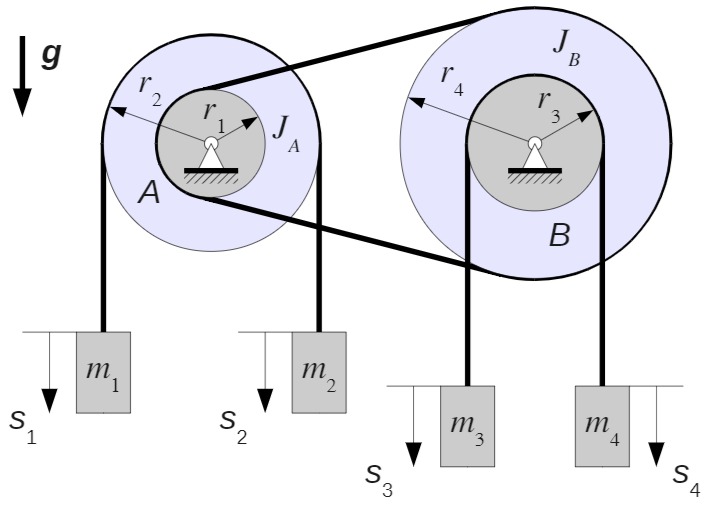 Die beiden Rollen
Die beiden Rollen
Über den äußeren Umfang der Rolle
Über den inneren Umfang der Rolle
Die Seile und der Riemen sind masselos.
- Geben Sie die Geschwindigkeiten
und der Massen bis sowie die Winkelgeschwindigkeiten und der Rollen und in Abhängigkeit von der Geschwindigkeit der Masse an. - Ermitteln Sie die Beschleunigungen
und der Massen sowie die Winkelbeschleunigungen und der Rollen. - Ermitteln Sie die Seilkräfte
bis in den Seilen, an denen die Massen hängen.
Gegeben:
Lösungsweg:
a) Kinematische Beziehungen
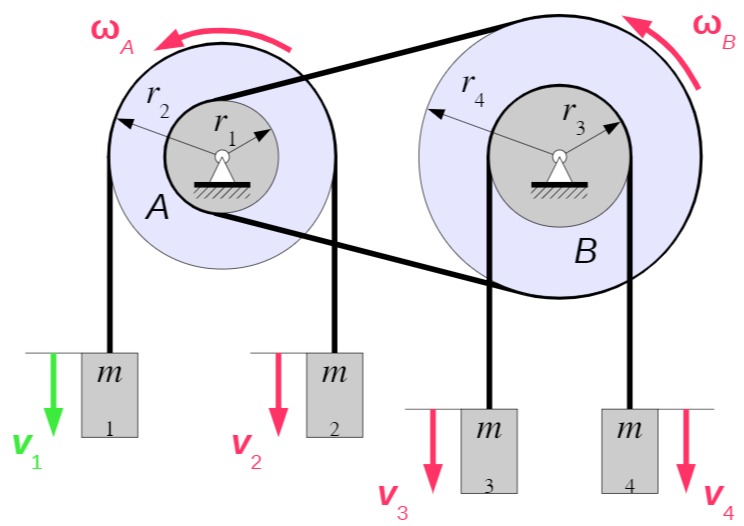
Rolle 1:
Rolle 2 :
Zahlenwerte:
b) Beschleunigungen und Winkelbeschleunigungen
Das System besteht aus starr miteinander verbundenen starren Körpern, und die einzige Kraft, die Arbeit verrichtet, ist die konservative Gewichtskraft. Das System kann also mit dem Energieerhaltungssatz berechnet werden. Dazu wird zunächst
Das Nullniveau für die Lageenergien der Massen wird jeweils in die Ruhelage gelegt. Dann ist die Gesamtenergie in der Ruhelage null, und der Energieerhaltungssatz lautet:
Kinetische Energie in der ausgelenkten Lage:
Lageenergie in der ausgelenkten Lage:
Mit
Einsetzen in den Energieerhaltungssatz ergibt:
Für die Beschleunigung von Masse 1 folgt:
Für die übrigen Beschleunigungen folgt aus den kinematischen Beziehungen:
Für die Winkelbeschleunigungen folgt aus den kinematischen Beziehungen:
Zahlenwerte:
c) Seilkräfte
Die Seilkräfte können aus den Schwerpunktsätzen für die Massen berechnet werden:
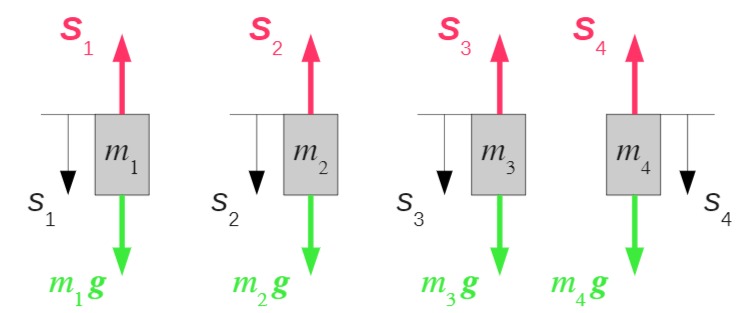
Daraus folgt:
Zahlenwerte: