Aufgabenstellung:
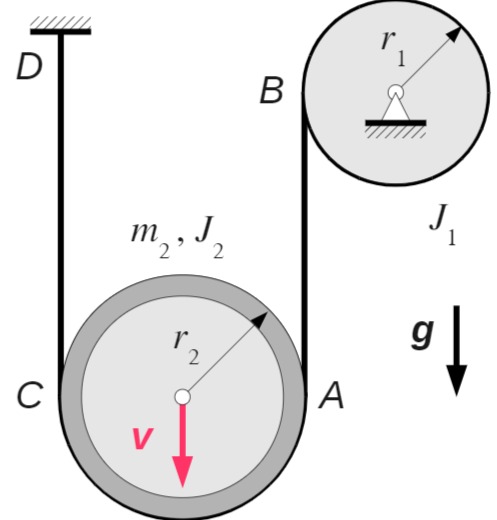
Das abgebildete System besteht aus der reibungsfrei gelenkig gelagerten Rolle
- Wie hängen die Winkelgeschwindigkeiten
und der beiden Rollen von der Geschwindigkeit ab, mit der sich die Rolle 2 nach unten bewegt? - Welche Beziehung gilt für die Geschwindigkeit
der Rolle 2 in Abhängigkeit vom zurückgelegten Weg wenn das System aus der Ruhe losgelassen wird? - Welche Beziehung gilt für die Beschleunigung
der Rolle - Welche Beziehungen gelten für die Kräfte
und in den Seilabschnitten und
Lösungsweg:
a) Kinematik
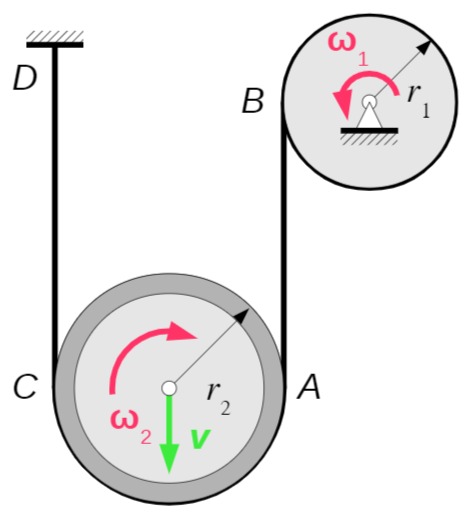
Die Rolle 2 rollt auf dem Seilstück
Da das Seil dehnstarr ist, gilt
Mit
b) Geschwindigkeit der Rolle 2
Die einzige am System angreifende äußere Kraft, die Arbeit verrichtet, ist die Gewichtskraft. Die Geschwindigkeit kann daher mit dem Energieerhaltungssatz bestimmt werden. Dazu wird das Nullniveau für die Lageenergie von Rolle 2 in die Ruhelage gelegt.
Es gilt für die einzelnen Energien:
Mit den kinematischen Beziehungen folgt für die kinetische Energie:
Der Energieerhaltungssatz lautet:
Einsetzen und auflösen nach der gesuchten Größe gibt:
c) Beschleunigung der Rolle 2
Die Beschleunigung der Rolle 2 berechnet sich zu
d) Seilkräfte
Die Seilkräfte können aus den kinetischen Gleichungen für die Rolle 2 berechnet werden.
Schwerpunktsatz in s-Richtung:
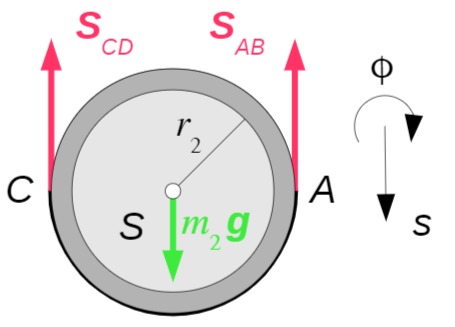
Drallsatz bezüglich Schwerpunkt S:
Kinematik:
Damit stehen zur Ermittlung der beiden Seilkräfte die folgenden beiden Gleichungen zur Verfügung:
Addition der beiden Gleichungen liefert
Daraus folgt
Subtraktion der ersten von der zweiten Gleichung ergibt
Daraus folgt
Einsetzen des Ergebnisses für die Beschleunigung führt auf