14 / 16

by Manfred Strohrmann

(H.ErT.Z-Online)

Aufgabenstellung:

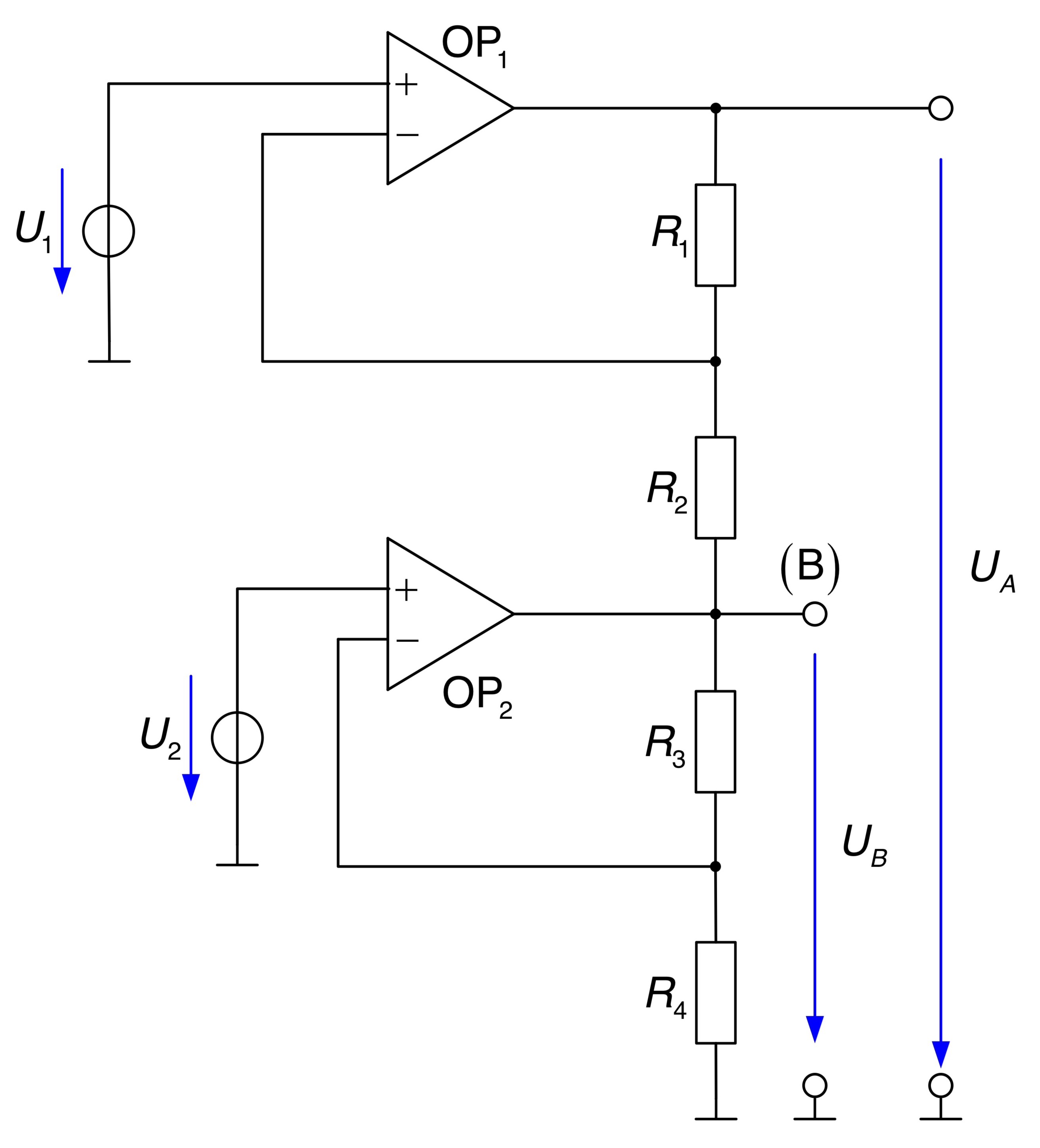
Für die folgende Schaltung soll die Ausgangsspannung bestimmt werden. Der Operationsverstärker kann als ideal angesehen werden und weist somit keinen Eingangsstrom und eine unendlich hohe offene Schleifenverstärkung auf.

  1. Berechnen Sie nach dem Superpositionsprinzip die Ausgangsspannung als Funktion der Eingangsspannungen und sowie der Widerstände bis .
  2. Mit einer besonderen Konstellation der Widerstände kann die in a) berechnete Gleichung für die Ausgangsspannung stark vereinfacht werden. Wie lautet diese Konstellation der Widerstände und zu welcher Gleichung führt sie?
  3. Welche Schaltungsfunktion kann die Schaltung mit der Dimensionierung nach b) erfüllen?

Abbildung

 

Lösungsweg:

Drücke auf "Aufdecken" um dir den ersten Schritt der Lösung anzuzeigen

a) Berechnen der Ausgangsspannung

  • Der Operationsverstärker bildet zusammen mit den Widerständen und einen einfachen nichtinvertierenden Verstärker.
  • Mit Hilfe der Standardgleichung für den nichtinvertierenden Verstärker kann eine Ersatzspannungsquelle im markierten Bereich gebildet werden.

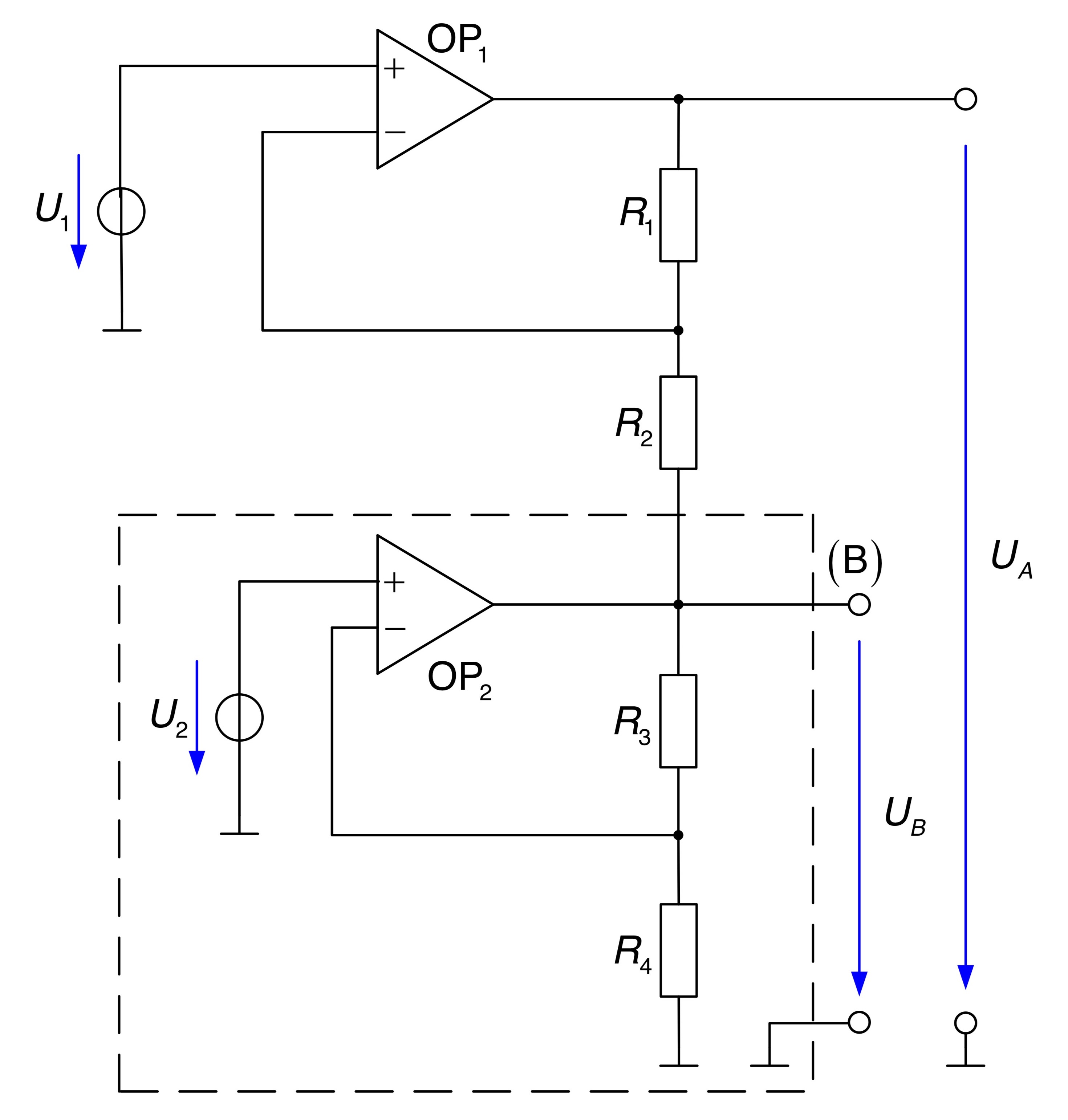
Abbildung

Die Gleichung für die Ersatzspannungsquelle lautet

  • Die Schaltung kann umgezeichnet werden.
  • Zur weiteren Berechnung der Schaltung wird das Superpositionsprinzip angewendet.

Abbildung

Zunächst wird die Spannung zu null gesetzt.

Die sich ergebende Schaltung ist ein einfacher nichtinvertierender Verstärker.

Wird die Spannungsquelle zu null gesetzt, entspricht die Schaltung einem einfachen invertierenden Verstärker.

Die Addition der Teilspannungen ergibt die Ausgangsspannung .

b) Bestimmen der Widerstandskonstelation

Die Gleichung der Ausgangsspannung wird zunächst ausmultipliziert.

Für das weitere Vorgehen wird die Annahme getroffen.

Wird diese Annahme in die Gleichung eingesetzt, ergibt sich

c) Bestimmen der Schaltungsfunktion

Mit dieser Schaltung kann eine Differenzbildung der beiden Spannungen und vorgenommen werden.

Gegenüber der Schaltung eines Subtrahierers ist der Eingangswiderstand unendlich, das heißt die beiden Spannungen und werden nicht belastet.

Lösung:

  3. Gegenüber der Schaltung eines Subtrahierers ist der Eingangswiderstand unendlich, das heißt die beiden Spannungen und werden nicht belastet.