Aufgabenstellung:
Die angegebene Schaltung stellt eine sogenannte Howland Strompumpe dar. Hierbei handelt es sich um eine spannungsgesteuerte Stromquelle mit Massebezug.
Der Operationsverstärker
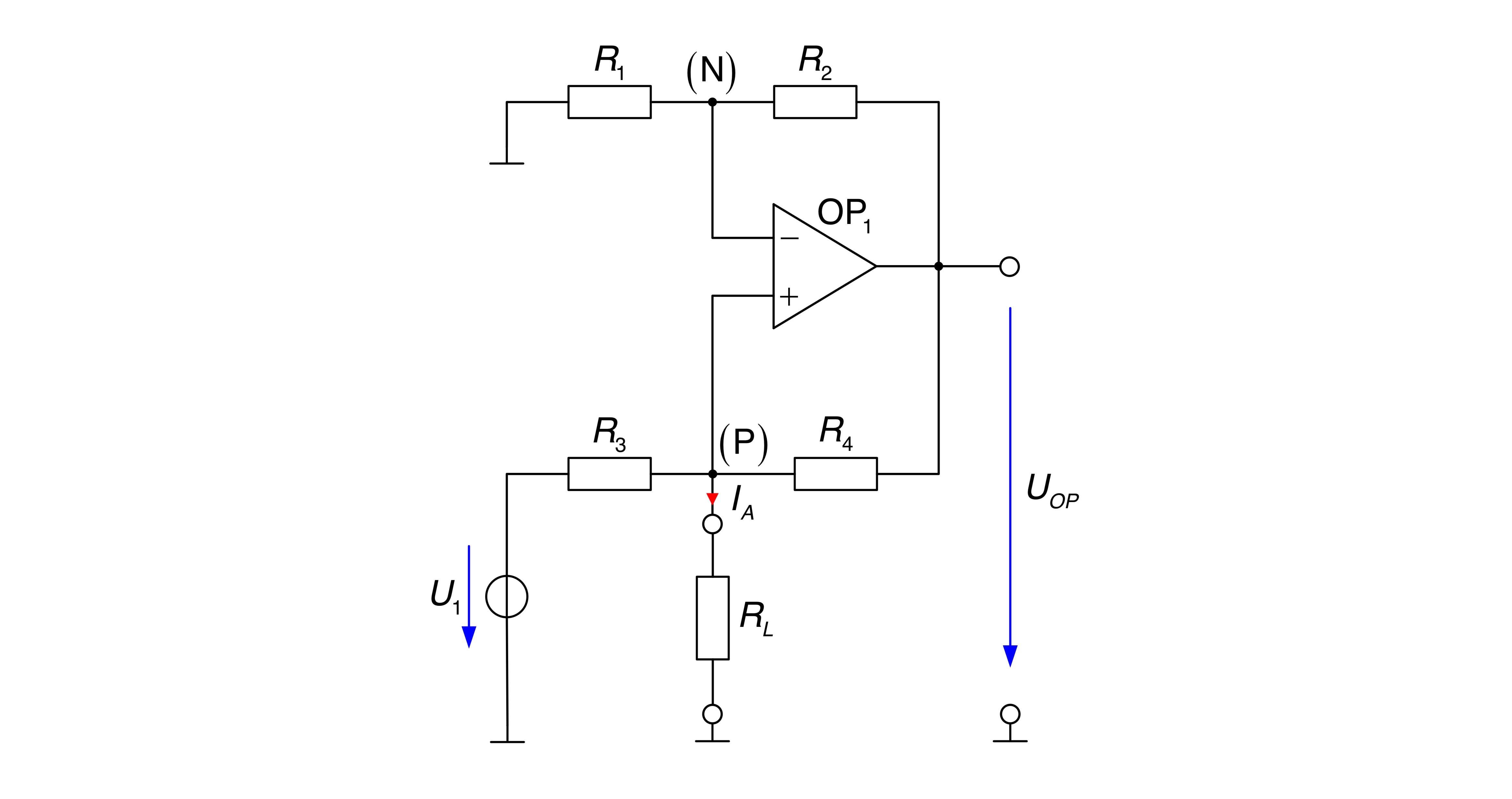
- Bestimmen Sie den Ausgangsstrom
in Abhängigkeit der Größen bis und . - Bei welcher Konstellation der Widerstände handelt es sich um eine ideale Stromquelle? Ist eine solche Umsetzung in der Praxis möglich?
- Berechnen Sie mit den folgenden Werten die maximale Spannung über dem Lastwiderstand
.
|
|
|
|
|
|
|
|
Lösungsweg:
a) Allgemeines Bestimmen von
In die Schaltung werden zunächst alle relevanten Zählpfeile eingetragen.
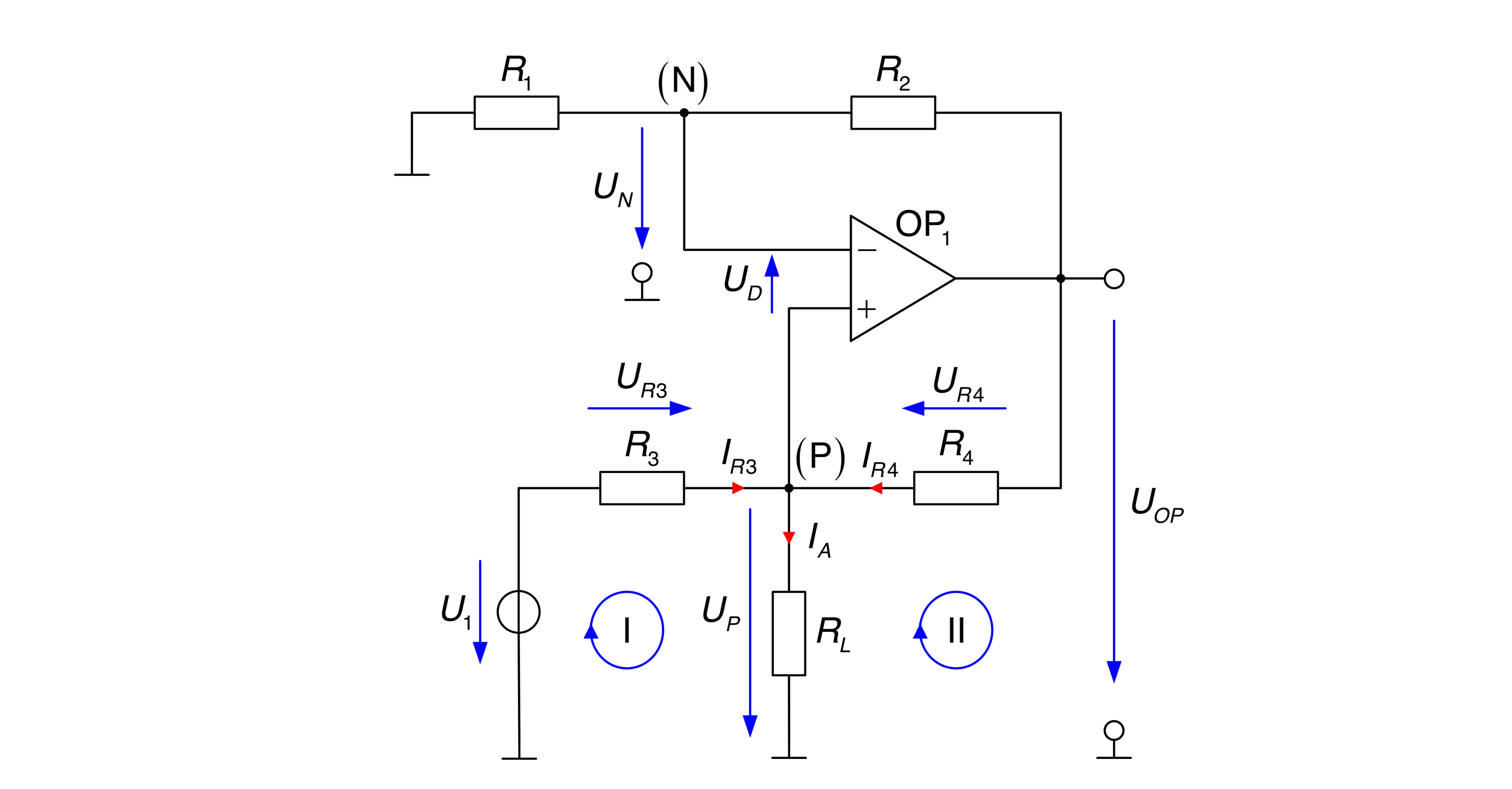
Da eine Gleichung für den Ausgangsstrom
Die Ströme
Es ergibt sich:
Zum Bestimmen der Spannungen werden zwei Maschengleichungen aufgestellt.
Für die Masche I ergibt sich die Gleichung
Die zweite Maschengleichung lautet
Bevor beide Gleichungen in die Knotenbilanz eingesetzt werden können, wird die Ausgangsspannung des Operationsverstärkers mit Hilfe der Knotenspannung
Da die Differenzspannung
Nach der Spannungsteilerregel gilt:
Auflösen nach der Spannung
Die zweite Maschengleichung lautet damit:
Die umgeformten Maschengleichungen werden in die zu Beginn aufgestellte Knotengleichung eingesetzt.
Es ergibt sich:
Da die Spannung
Die Gleichung wird nach dem Ausgangsstrom aufgelöst.
b) Bestimmen der Widerstandskonstelation
Ist eine Quelle von der Belastung unabhängig, handelt es sich um eine ideale Quelle.
Die in Aufgabenteil a) bestimmte Gleichung darf somit keine Abhängigkeit zum Lastwiderstand
Somit muss der Ansatz gelten:
Hiermit ergibt sich das Widerstandsverhältnis
Mit dieser Anordnung ergibt sich der Ausgangsstrom zu
Die umgeformten Maschengleichungen werden in die zu Beginn aufgestellte Knotengleichung eingesetzt.
Es ergibt sich:
Da die Spannung
Die Gleichung wird nach dem Ausgangsstrom aufgelöst.
b) Ist eine solche Umsetzung in der Praxis möglich?
Ist eine Quelle von der Belastung unabhängig, handelt es sich um eine ideale Quelle.
Die in Aufgabenteil a) bestimmte Gleichung darf somit keine Abhängigkeit zum Lastwiderstand
Somit muss der Ansatz gelten:
Hiermit ergibt sich das Widerstandsverhältnis
Mit dieser Anordnung ergibt sich der Ausgangsstrom zu
Wird ein solches Verhältnis der Widerstände gewählt, handelt es sich rechnerisch um eine ideale Stromquelle.
Da sich in der Praxis der Anspruch der völligen Gleichheit der Widerstände nicht einhalten lässt, wird die reale Schaltung einen Innenwiderstand
c) Berechnung der maximalen Spannung am Lastwiderstand
Da es sich um eine ideale Stromquelle handelt, bleibt der Ausgangsstrom bei veränderlichem Lastwiderstand konstant und berechnet sich zu
Bei konstantem Strom ergibt sich der maximale Spannungswert bei dem größten Widerstandswert.
