Aufgabenstellung:
Gegeben ist eine Schaltungsanordnung bestehend aus zwei idealen Operationsverstärkern, zwei Spannungsquellen und Widerständen.
Geben Sie die Spannungen
Verwenden Sie hierzu das Superpositionsprinzip.
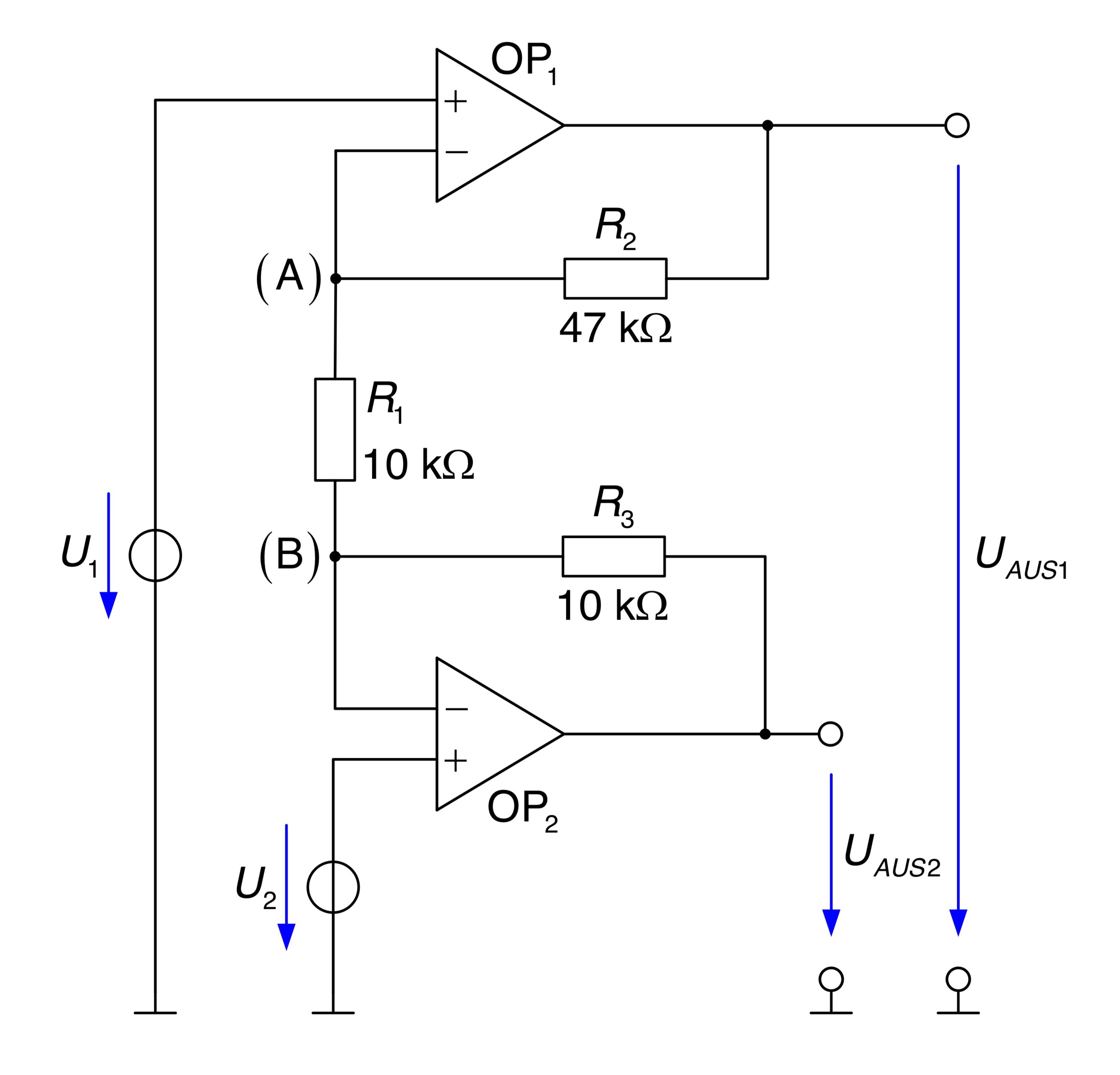
Lösungsweg:
Bestimmen der Spannungen
- Zur Berechnung der beiden Ausgangsspannungen
und wird das Superpositionsprinzip verwendet. - Zunächst werden die Knotenspannungen
und in die Schaltung eingezeichnet.
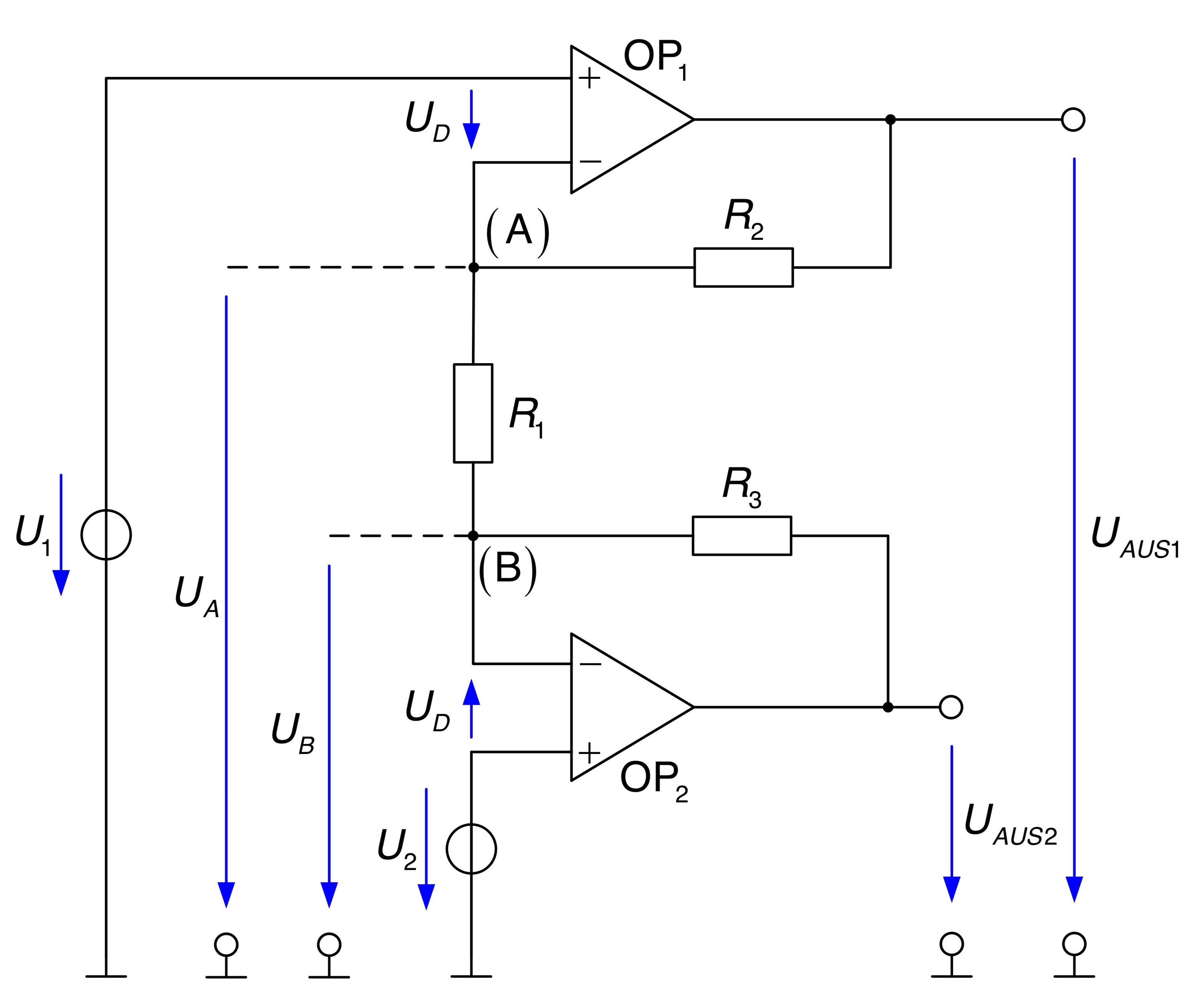
Durch die unendliche Verstärkung sind die Differenzspannungen an den Eingängen der Operationsverstärker null.
Als Hilfsgrößen werden die eingezeichneten Knotenspannungen
Die Maschengleichung für die Spannung am Knoten (A) lautet
beziehungsweise für den Knoten (B)
Zunächst wird die Spannungsquelle
Es gilt
Die zuvor bestimmten Knotengleichungen ergeben sich zu:
beziehungsweise
Der Operationsverstärker OP
Die erste Teilspannung der Ausgangsspannung 1 berechnet sich zu:
Der Operationsverstärker
Die zweite Ausgangsspannung lautet:
Zur Berechnung der jeweils zweiten Teilspannung wird die Spannungsquelle
Es gilt
Die Maschengleichungen ergeben sich zu
beziehungsweise
Mit den Widerständen
Die erste Ausgangsspannung berechnet sich zu:
Der Operationsverstärker OP
Die Überlagerung der Teilspannungen führt zum Ergebnis der jeweiligen Ausgangsspannung.
Einsetzen der Zahlenwerte ergibt:
