Aufgabenstellung:
Gegeben ist ein System aus drei gelenkig verbundenen Stäben. Das System liegt dabei unter der Belastung durch die beiden Kräfte
- Berechne das Verhältnis
der Kräfte. - Wie groß sind die Stabkräfte
und in Abhängigkeit der angreifenden Kraft

Lösungsweg:
1. Kräfteverhältnis:
Schneide nacheinander die Gelenke
Schneidest du die Gelenke frei, so liegen jeweils zentrale Kräftesysteme vor, für die jeweils zwei Gleichgewichtsbedingungen gelten.
Für
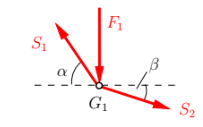
Forme die Gleichungen nach der Stabkraft
Für
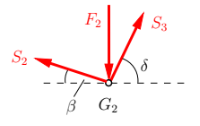
Löse auch hier wieder die Gleichungen nach der Stabkraft
Somit liegen zwei Teillösungen für
Das Verhältnis der angreifenden Lasten
Bestimme noch aus der Geometrie der Gleichgewichtslage die unbekannten Winkel:
Setze alles in die gefundenen Formel für das Kräfteverhältnis ein:
2. Stabkräfte:
Ermittel zunächst
Lösung: