Aufgabenstellung:
Es sei die Menge
Bestimme alle Elemente der Menge
Lösungsweg:
Drücke auf "Aufdecken" um dir den ersten Schritt der Lösung anzuzeigen
Setze ein:
Um den Betrag einer komplexen Zahl aufzulösen, identifiziere zunächst Real-und Imaginärteil!
Um die Ungleichung zu quadrieren, überprüfe, ob beide Seiten
Da beide Seiten der Ungleichung
Vereinfache den Ausdruck um deine Lösungsmenge zu erhalten:
Welcher Geometrischen Form entspricht dieses Ergebnis? Skizziere:
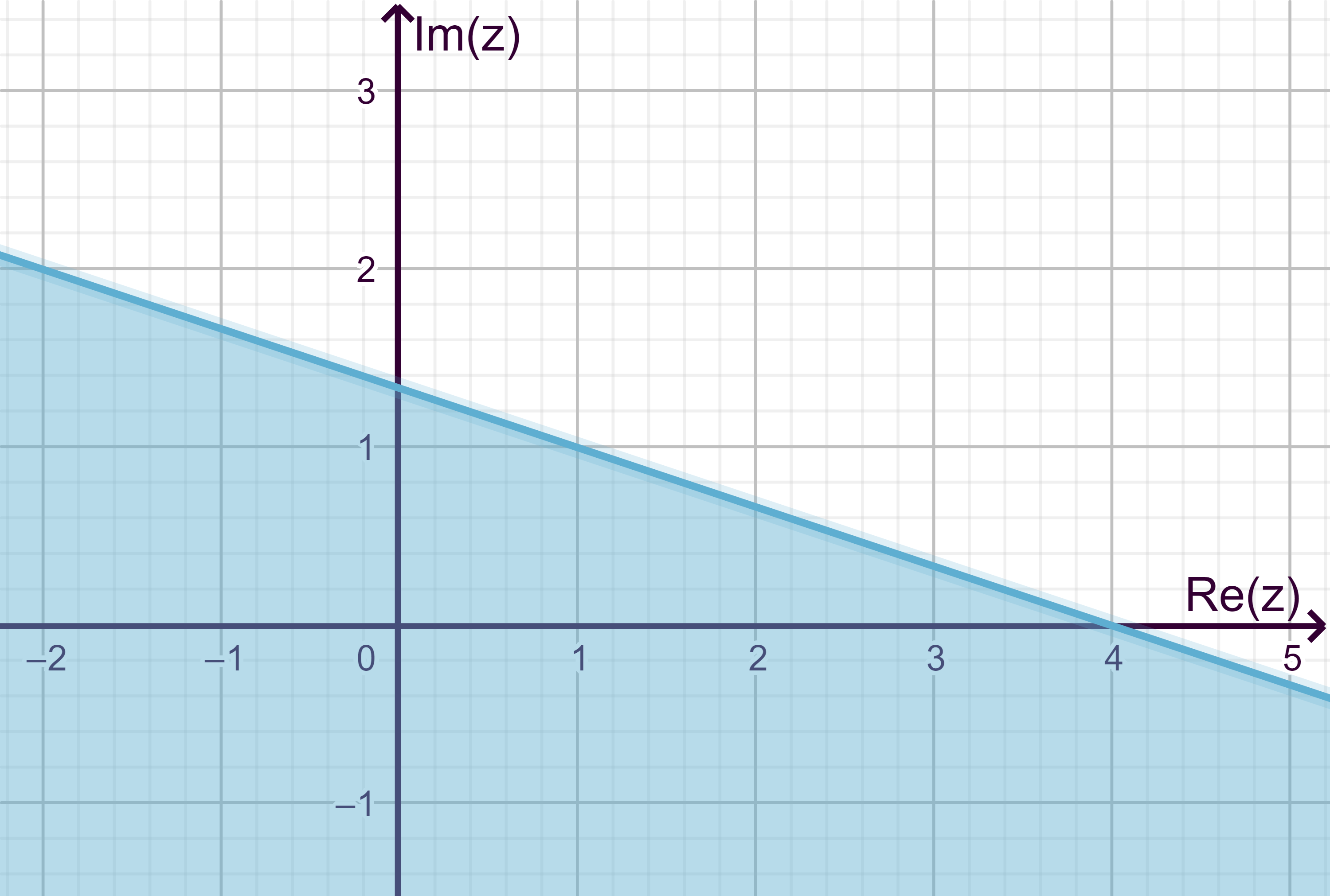
Lösung:
Die Menge