Aufgabenstellung:
Ermitteln Sie durch Betrachtung der Winkel im gleichseitigen bzw. im gleichschenkligen rechtwinkligen Dreieck den Sinus, Kosinus und Tangens von
Lösungsweg:
Da im gleichseitigen Dreieck Winkelhalbierende und Mittelsenkrechte zusammenfallen, wird dieses durch eine solche Linie in zwei rechtwinklige Dreiecke mit Winkeln von
Skizze
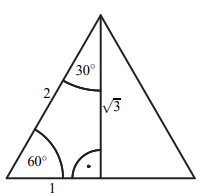
Folglich gilt
Das gleichschenklige rechtwinklige Dreieck hat zwei Winkel von
Skizze
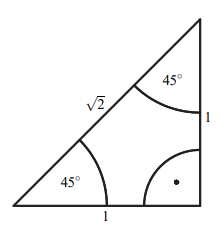
Folglich gilt
Zusammengefasst kann man festhalten:
oder (wenn man will)