3 / 8

Aufgabenstellung:

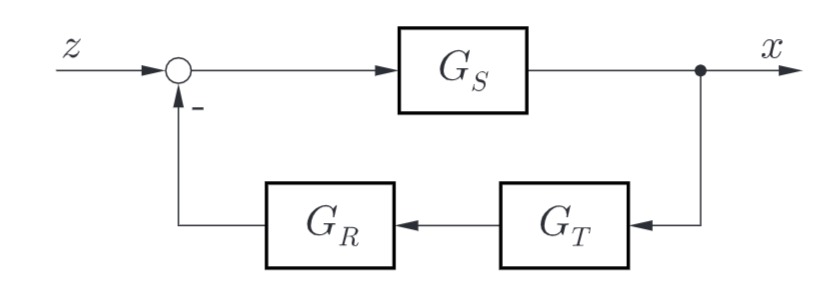AbbildungBetrachtet wird der folgende Regelkreis mit Der Frequenzgang der Regelstrecke ist ein reines Verzögerungselement dritter Ordnung.

 

 

 

Gegeben ist zudem die Ortskurve von mit sec:

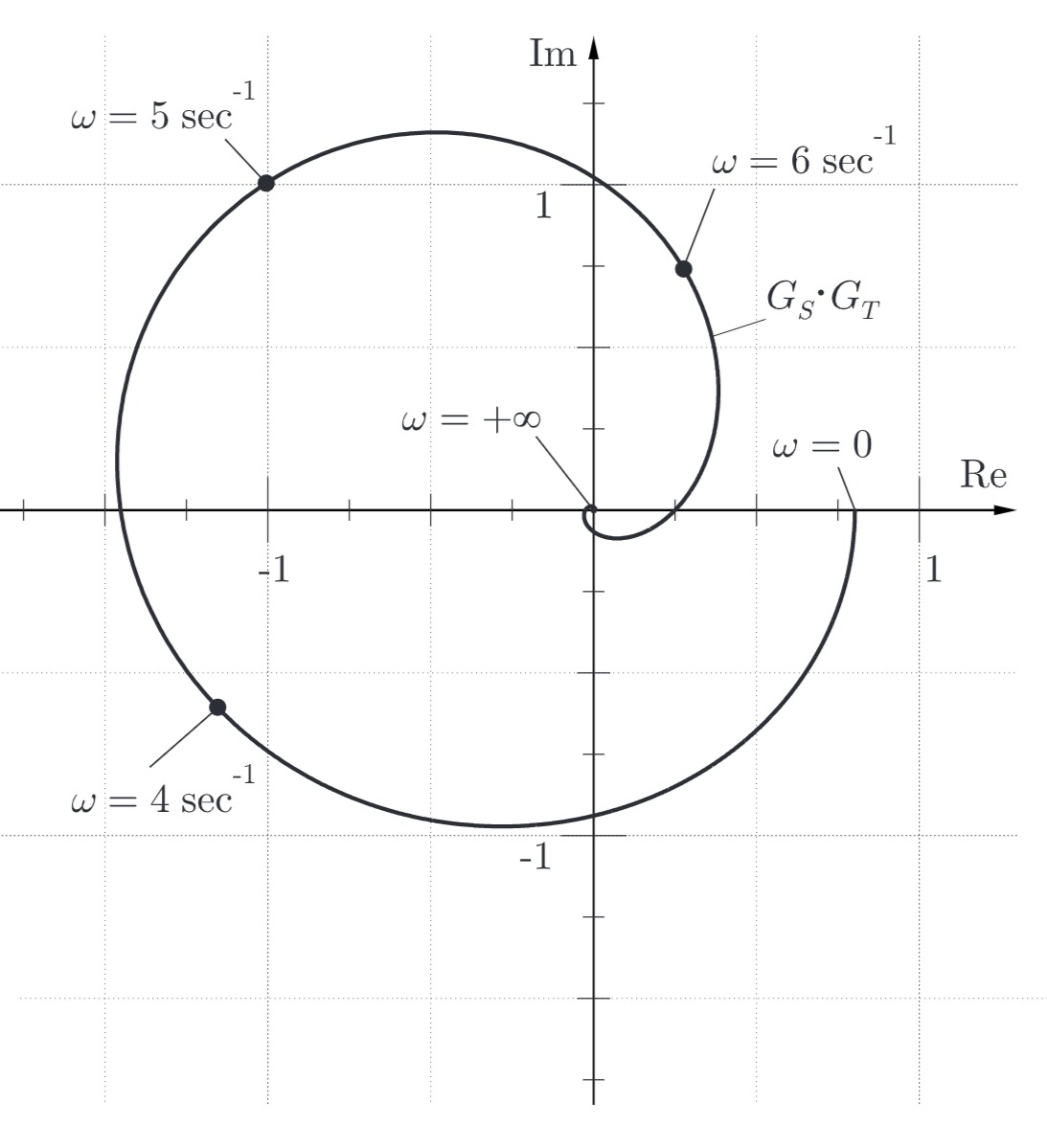
Abbildung

a) Skizzieren Sie den Verlauf der Ortskurve von in obigem Diagramm. Bestimmen Sie dazu Stützstellen mit Hilfe der gegebenen Punkte der Ortskurve von . Markieren Sie die Punkte mit der jeweiligen Frequenz.

Im Folgenden gilt:

b) Es gilt zunächst: . Weisen Sie nach, dass die Voraussetzungen für die Anwendbarkeit des vereinfachten Nyquist-Kriteriums zur Beurteilung der Stabilität des Regelkreises erfüllt sind. Ist der geschlossene Regelkreis stabil?

Es soll nun ein -Regler zum Einsatz kommen: Der Regler soll so ausgelegt werden, dass der geschlossene Regelkreis eine Amplitudenreserve von bei der Frequenz aufweist.

c) Bestimmen Sie die Parameter und des -Reglers.

Lösungsweg:

Drücke auf "Aufdecken" um dir den ersten Schritt der Lösung anzuzeigen

a) Ortskurve von

Bestimmung der Stützpunkte für die gegebenen Frequenzen aus Ortskurve von :

Betrag:

Da für alle

Phase:

Skizze

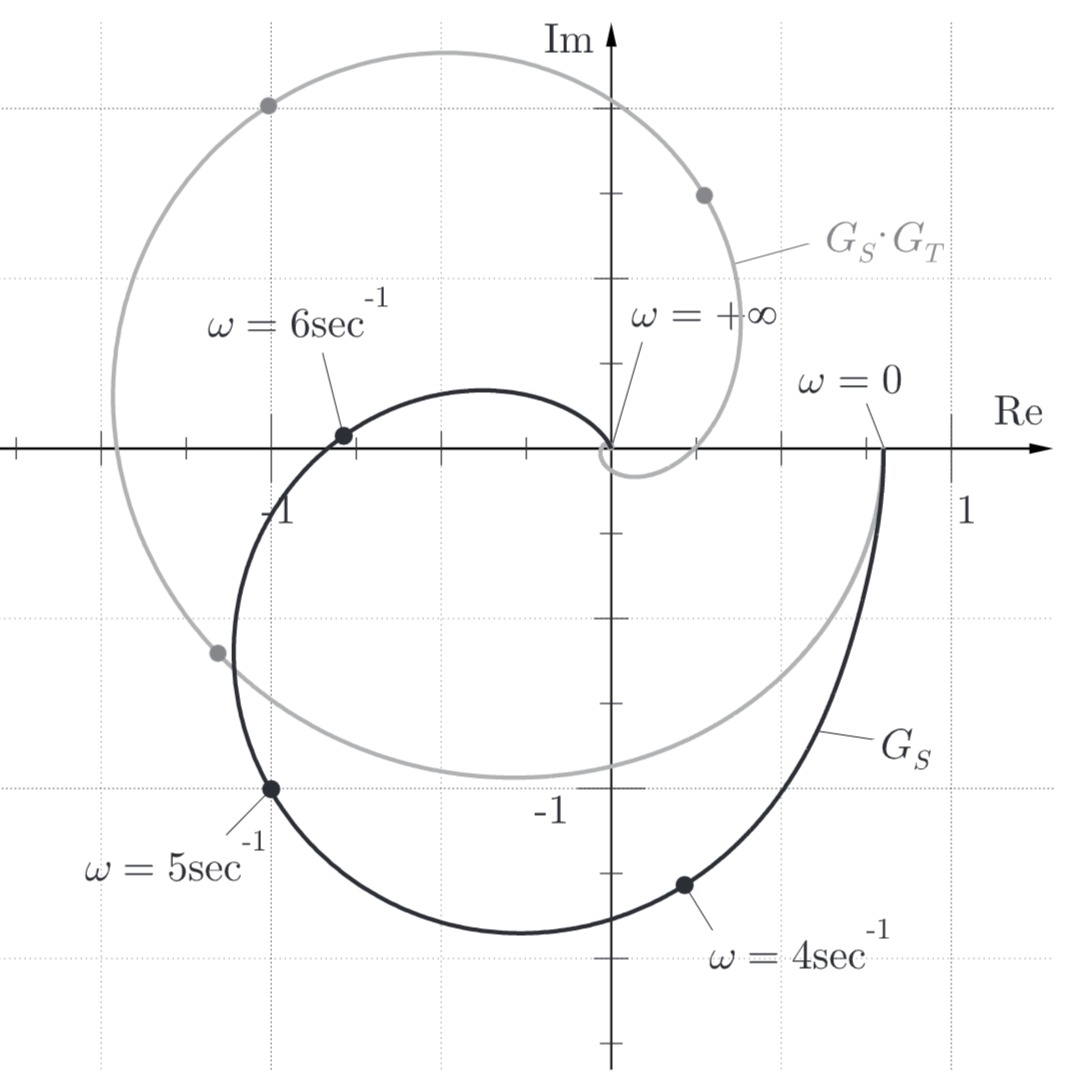
Abbildung

b) Anwendbarkeit des vereinfachten Nyquist-Kriteriums

1. Prüfe: Der aufgeschnittene Regelkreis muss stabil sein oder integrierendes Verhalten aufweisen.

hat drei stabile Polstellen (s. Aufgabenstellung und Ortskurve: 3 Polstellen, Phase fällt um , ist stabil.
Der aufgeschnittene Regelkreis ist eine Reihenschaltung stabiler Glieder und damit stabil.
Die Bedingung ist erfüllt.

2. Prüfe: Die Ortskurve des Frequenzgangs darf die reelle Achse nur so schneiden, dass die Frequenz beim Übergang vom dritten in den zweiten Quadranten zunimmt.

streckt Ortskurve von lediglich um Faktor 2.
Die Bedingung ist erfüllt.

Anwendung des vereinfachten Nyquist-Kriteriums:

schneidet die reelle Achse links der

Der geschlossene Regelkreis ist instabil.

c) Parameter und des -Reglers bestimmen

Bestimmung von

Bestimmung von  

Lösung:

  1. siehe Musterlösung 
  2. Der geschlossene Regelkreis ist instabil.
  3. ;