1 / 8

Aufgabenstellung:

Betrachtet wird der folgende Regelkreis:

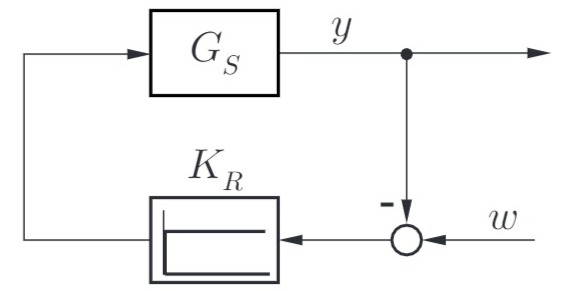
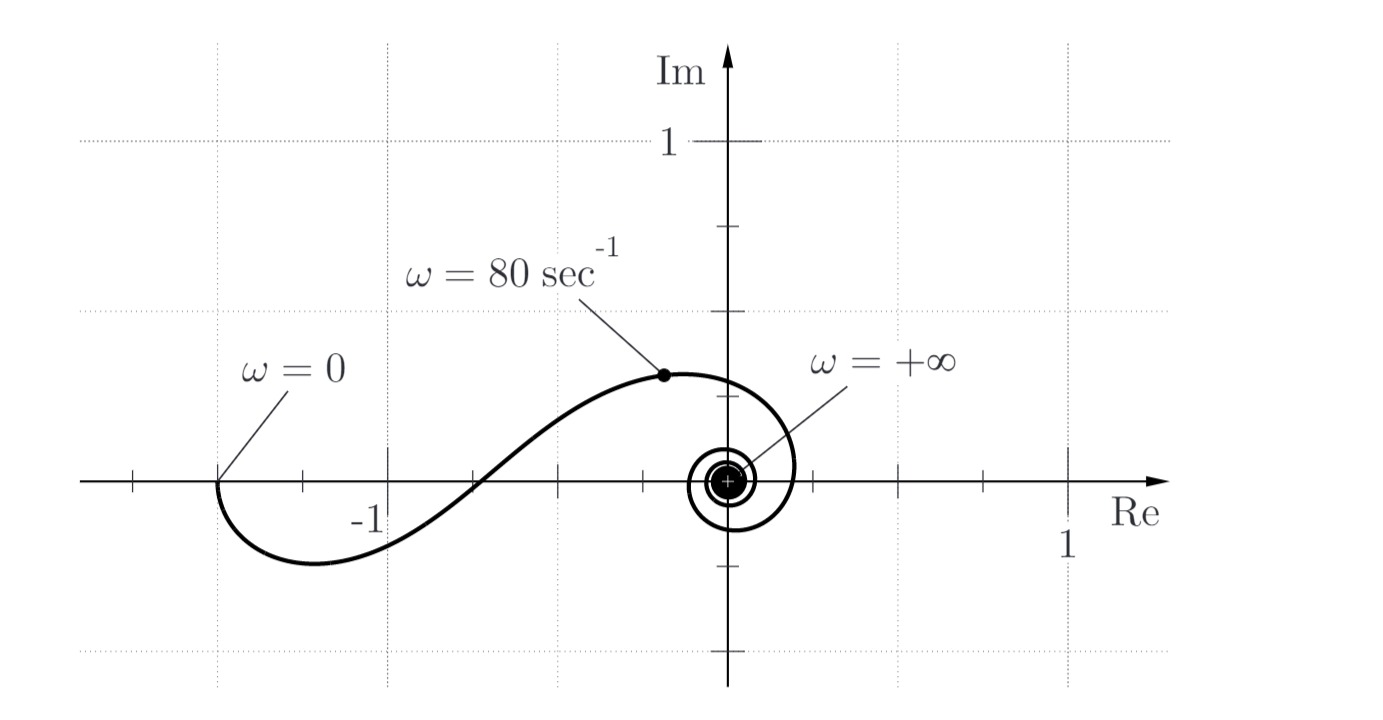
Abbildung

Gegeben ist die Ortskurve der Strecke mit dem Frequenzgang

Abbildung

Für den Regler gilt:

  1. Bestimmen Sie .
  2. Ist der geschlossene Regelkreis für stabil?
  3. Bestimmen Sie den Wertebereich von , für den der geschlossene Regelkreis stabil ist.
  4. Bestimmen Sie die Totzeit

Lösungsweg:

Drücke auf "Aufdecken" um dir den ersten Schritt der Lösung anzuzeigen

a) besimmen

Bestimmen des Grenzwertes von für (aus Ortskurve abgelesen):

b) Stabilität prüfen

Anwenden des vollständigen Nyquistkriteriums auf den aufgeschnittenen Regelkreis:

  • besitzt 1 instabilen
  • die Ortskurve von umrundet den Punkt einmal im mathematisch positiven Sinn für

mit folgt, dass der geschlossene Regelkreis mit keine Pole in der rechten -Halbebene hat und somit stabil ist.

c) Wertebereich von

Aus b) ist bekannt, um den geschlossenen Regelkreis zu stabilisieren, muss gelten:

  • dies ist der Fall, solange der linke »Bauch « den Punkt umschlieft

für folgt:

d) Totzeit

Für die Phase von gilt:

bei lässt sich aus der Ortskurve ablesen

Unter Berücksichtigung der entsprechenden Quadranten lässt sich die Phase des -Elements bei berechnen:

Daraus folgt für die (Phase der) Totzeit:

Lösung:

  2. stabil