MIMO-System

Sensitivität

Sprungfunktion

Schwingung

Laplace-Transformation

Linearisierung nichtlinearer Systeme

Unterschied In/Homogen

Basis, Basiswechsel

Abbildungsmatrizen

Funktionen bestimmen

Geraden und Ebenen

Gruppen

lineare abbildung 

quadratische ergänzung

Baustatik 1

Anfangswertprobleme :)

Differentialgleichungen

basis 

QR-Algorithmus

QR-Zerlegung

Cholesky-Zerlegung

Bild & Urbild

Zweigstromanalyse

Transistor als Thermometer

Investment

Teilfolgen

Epsilon Delta Kriterium

prinzip der virtuellen verrückung 

Linear Kombination

Folgen, Reihen und Potenzreihen

Flächenpressung

Arbeit 

Cholesky Zerlegung

Polynomfunktionen beschreiben

Zu Maß-und Integrationstheorie: Majorisierte Konvergenz

Teilchenphysik und Festkörperphysik

Orthogonaltrajektorien

test

Taylorreihen

Regel von de L'Hopital

Mathe

KRAFT

Grenzwert Funktion 

Folgenkriterium

ϵ-δ Kriterium 

Beweis Stetigkeit 

Wahrheitstabelle

2x2 Matrix

Matrix invertieren

Basiswechselsatz

Lineare Abbildunge 

Vorderrad fahradgabel lagerkräfte berechnen 

Spannungsregelung

Jordan Normal Form

Test

Induktion 

Jordan-Normalform

Ansatz der Störfunktion zur Bestimmung der Partikulären Lösung

Kurvenintegral

dlg mithilfe inhomogenen linearen system lösen

Inverse einer Matrix

Gleichmäßige Stetigkeit

addition

Regel von L´Hospital

Lineare Abbildungen

dimension eines Untervektorraumes bestimmen

Stationäre Stoffübertragung

Polplan, Prinzip der virtuellen Verrückungen

komplexe Ungleichungen 

Bidualräume

Dualräume

Taylorpolynome

Kern und Basis

Diagonalisieren einer Matrix

Rekursive Folgen

Exponentialreihe

Darstellungsmatrizen

restglied

Basiswechsel

Gamma Funktion

Newton Verfahren

Randwertaufgabe

Numerische Integration: Trapez- und Simpsonregel

Funktionenfolgen

dualräume

Dualraum

Komplexe Nullstellen

Chemie

Natascha Kirchmann

Differentialquotient

Folgedefinition des Funktionslimes

Grenzwerte und Stetigkeit 

Komplexe Zahlen

Kern und Bild 

Direkte Summe 

Koordinaten 

Exponentielle Verzinsung

Lineare Verzinsung

Festverzinsliche Wertpapiere

<ol style="list-style-type: lower-alpha;">
<li>\( \lim _{t \rightarrow \infty} x(t) \) existiert nicht</li>
<li>\[<br />G_{S}(j \omega)=\frac{4 \sec ^{-2}}{(j \omega)^{2}+2 \sec \cdot(j \omega)^{3}} <br />\]</li>
<li>\[<br />0,055 \mathrm{sec} \leq K_{R} \leq 0,13 \mathrm{sec} <br />\]</li>
</ol>

<p>a)  stationärer Endwert \( \lim _{t \rightarrow \infty} x(t) \)</p>


<p>a)  stationärer Endwert <mjx-container class="MathJax" jax="SVG"><svg alt=" \lim _{t \rightarrow \infty} x(t) " style="vertical-align: -0.566ex" xmlns="http://www.w3.org/2000/svg" width="11.356ex" height="2.262ex" role="img" focusable="false" viewBox="0 -750 5019.1 1000" xmlns:xlink="http://www.w3.org/1999/xlink"><defs><path id="MJX-2260-TEX-N-6C" d="M42 46H56Q95 46 103 60V68Q103 77 103 91T103 124T104 167T104 217T104 272T104 329Q104 366 104 407T104 482T104 542T103 586T103 603Q100 622 89 628T44 637H26V660Q26 683 28 683L38 684Q48 685 67 686T104 688Q121 689 141 690T171 693T182 694H185V379Q185 62 186 60Q190 52 198 49Q219 46 247 46H263V0H255L232 1Q209 2 183 2T145 3T107 3T57 1L34 0H26V46H42Z"></path><path id="MJX-2260-TEX-N-69" d="M69 609Q69 637 87 653T131 669Q154 667 171 652T188 609Q188 579 171 564T129 549Q104 549 87 564T69 609ZM247 0Q232 3 143 3Q132 3 106 3T56 1L34 0H26V46H42Q70 46 91 49Q100 53 102 60T104 102V205V293Q104 345 102 359T88 378Q74 385 41 385H30V408Q30 431 32 431L42 432Q52 433 70 434T106 436Q123 437 142 438T171 441T182 442H185V62Q190 52 197 50T232 46H255V0H247Z"></path><path id="MJX-2260-TEX-N-6D" d="M41 46H55Q94 46 102 60V68Q102 77 102 91T102 122T103 161T103 203Q103 234 103 269T102 328V351Q99 370 88 376T43 385H25V408Q25 431 27 431L37 432Q47 433 65 434T102 436Q119 437 138 438T167 441T178 442H181V402Q181 364 182 364T187 369T199 384T218 402T247 421T285 437Q305 442 336 442Q351 442 364 440T387 434T406 426T421 417T432 406T441 395T448 384T452 374T455 366L457 361L460 365Q463 369 466 373T475 384T488 397T503 410T523 422T546 432T572 439T603 442Q729 442 740 329Q741 322 741 190V104Q741 66 743 59T754 49Q775 46 803 46H819V0H811L788 1Q764 2 737 2T699 3Q596 3 587 0H579V46H595Q656 46 656 62Q657 64 657 200Q656 335 655 343Q649 371 635 385T611 402T585 404Q540 404 506 370Q479 343 472 315T464 232V168V108Q464 78 465 68T468 55T477 49Q498 46 526 46H542V0H534L510 1Q487 2 460 2T422 3Q319 3 310 0H302V46H318Q379 46 379 62Q380 64 380 200Q379 335 378 343Q372 371 358 385T334 402T308 404Q263 404 229 370Q202 343 195 315T187 232V168V108Q187 78 188 68T191 55T200 49Q221 46 249 46H265V0H257L234 1Q210 2 183 2T145 3Q42 3 33 0H25V46H41Z"></path><path id="MJX-2260-TEX-I-1D461" d="M26 385Q19 392 19 395Q19 399 22 411T27 425Q29 430 36 430T87 431H140L159 511Q162 522 166 540T173 566T179 586T187 603T197 615T211 624T229 626Q247 625 254 615T261 596Q261 589 252 549T232 470L222 433Q222 431 272 431H323Q330 424 330 420Q330 398 317 385H210L174 240Q135 80 135 68Q135 26 162 26Q197 26 230 60T283 144Q285 150 288 151T303 153H307Q322 153 322 145Q322 142 319 133Q314 117 301 95T267 48T216 6T155 -11Q125 -11 98 4T59 56Q57 64 57 83V101L92 241Q127 382 128 383Q128 385 77 385H26Z"></path><path id="MJX-2260-TEX-N-2192" d="M56 237T56 250T70 270H835Q719 357 692 493Q692 494 692 496T691 499Q691 511 708 511H711Q720 511 723 510T729 506T732 497T735 481T743 456Q765 389 816 336T935 261Q944 258 944 250Q944 244 939 241T915 231T877 212Q836 186 806 152T761 85T740 35T732 4Q730 -6 727 -8T711 -11Q691 -11 691 0Q691 7 696 25Q728 151 835 230H70Q56 237 56 250Z"></path><path id="MJX-2260-TEX-N-221E" d="M55 217Q55 305 111 373T254 442Q342 442 419 381Q457 350 493 303L507 284L514 294Q618 442 747 442Q833 442 888 374T944 214Q944 128 889 59T743 -11Q657 -11 580 50Q542 81 506 128L492 147L485 137Q381 -11 252 -11Q166 -11 111 57T55 217ZM907 217Q907 285 869 341T761 397Q740 397 720 392T682 378T648 359T619 335T594 310T574 285T559 263T548 246L543 238L574 198Q605 158 622 138T664 94T714 61T765 51Q827 51 867 100T907 217ZM92 214Q92 145 131 89T239 33Q357 33 456 193L425 233Q364 312 334 337Q285 380 233 380Q171 380 132 331T92 214Z"></path><path id="MJX-2260-TEX-I-1D465" d="M52 289Q59 331 106 386T222 442Q257 442 286 424T329 379Q371 442 430 442Q467 442 494 420T522 361Q522 332 508 314T481 292T458 288Q439 288 427 299T415 328Q415 374 465 391Q454 404 425 404Q412 404 406 402Q368 386 350 336Q290 115 290 78Q290 50 306 38T341 26Q378 26 414 59T463 140Q466 150 469 151T485 153H489Q504 153 504 145Q504 144 502 134Q486 77 440 33T333 -11Q263 -11 227 52Q186 -10 133 -10H127Q78 -10 57 16T35 71Q35 103 54 123T99 143Q142 143 142 101Q142 81 130 66T107 46T94 41L91 40Q91 39 97 36T113 29T132 26Q168 26 194 71Q203 87 217 139T245 247T261 313Q266 340 266 352Q266 380 251 392T217 404Q177 404 142 372T93 290Q91 281 88 280T72 278H58Q52 284 52 289Z"></path><path id="MJX-2260-TEX-N-28" d="M94 250Q94 319 104 381T127 488T164 576T202 643T244 695T277 729T302 750H315H319Q333 750 333 741Q333 738 316 720T275 667T226 581T184 443T167 250T184 58T225 -81T274 -167T316 -220T333 -241Q333 -250 318 -250H315H302L274 -226Q180 -141 137 -14T94 250Z"></path><path id="MJX-2260-TEX-N-29" d="M60 749L64 750Q69 750 74 750H86L114 726Q208 641 251 514T294 250Q294 182 284 119T261 12T224 -76T186 -143T145 -194T113 -227T90 -246Q87 -249 86 -250H74Q66 -250 63 -250T58 -247T55 -238Q56 -237 66 -225Q221 -64 221 250T66 725Q56 737 55 738Q55 746 60 749Z"></path></defs><g stroke="currentColor" fill="currentColor" stroke-width="0" transform="scale(1,-1)"><g data-mml-node="math"><g data-mml-node="munder"><g data-mml-node="mo"><use data-c="6C" xlink:href="#MJX-2260-TEX-N-6C"></use><use data-c="69" xlink:href="#MJX-2260-TEX-N-69" transform="translate(278,0)"></use><use data-c="6D" xlink:href="#MJX-2260-TEX-N-6D" transform="translate(556,0)"></use></g><g data-mml-node="TeXAtom" transform="translate(1422,-150) scale(0.707)" data-mjx-texclass="ORD"><g data-mml-node="mi"><use data-c="1D461" xlink:href="#MJX-2260-TEX-I-1D461"></use></g><g data-mml-node="mo" transform="translate(361,0)"><use data-c="2192" xlink:href="#MJX-2260-TEX-N-2192"></use></g><g data-mml-node="mi" transform="translate(1361,0)"><use data-c="221E" xlink:href="#MJX-2260-TEX-N-221E"></use></g></g></g><g data-mml-node="mi" transform="translate(3308.1,0)"><use data-c="1D465" xlink:href="#MJX-2260-TEX-I-1D465"></use></g><g data-mml-node="mo" transform="translate(3880.1,0)"><use data-c="28" xlink:href="#MJX-2260-TEX-N-28"></use></g><g data-mml-node="mi" transform="translate(4269.1,0)"><use data-c="1D461" xlink:href="#MJX-2260-TEX-I-1D461"></use></g><g data-mml-node="mo" transform="translate(4630.1,0)"><use data-c="29" xlink:href="#MJX-2260-TEX-N-29"></use></g></g></g></svg></mjx-container></p>


<p>Aus Betrags- und Phasenverlauf erkennbar:</p>


<p>\(<br />G_{0, K_{R}=1 \mathrm{sec}} \) besitzt integrierendes Verhalten \( \left(I T_{2}\right) <br />\)</p>


<p><mjx-container class="MathJax" jax="SVG"><svg alt="
G_{0, K_{R}=1 \mathrm{sec}} " style="vertical-align: -0.65ex" xmlns="http://www.w3.org/2000/svg" width="9.656ex" height="2.245ex" role="img" focusable="false" viewBox="0 -705 4267.8 992.2" xmlns:xlink="http://www.w3.org/1999/xlink"><defs><path id="MJX-2261-TEX-I-1D43A" d="M50 252Q50 367 117 473T286 641T490 704Q580 704 633 653Q642 643 648 636T656 626L657 623Q660 623 684 649Q691 655 699 663T715 679T725 690L740 705H746Q760 705 760 698Q760 694 728 561Q692 422 692 421Q690 416 687 415T669 413H653Q647 419 647 422Q647 423 648 429T650 449T651 481Q651 552 619 605T510 659Q492 659 471 656T418 643T357 615T294 567T236 496T189 394T158 260Q156 242 156 221Q156 173 170 136T206 79T256 45T308 28T353 24Q407 24 452 47T514 106Q517 114 529 161T541 214Q541 222 528 224T468 227H431Q425 233 425 235T427 254Q431 267 437 273H454Q494 271 594 271Q634 271 659 271T695 272T707 272Q721 272 721 263Q721 261 719 249Q714 230 709 228Q706 227 694 227Q674 227 653 224Q646 221 643 215T629 164Q620 131 614 108Q589 6 586 3Q584 1 581 1Q571 1 553 21T530 52Q530 53 528 52T522 47Q448 -22 322 -22Q201 -22 126 55T50 252Z"></path><path id="MJX-2261-TEX-N-30" d="M96 585Q152 666 249 666Q297 666 345 640T423 548Q460 465 460 320Q460 165 417 83Q397 41 362 16T301 -15T250 -22Q224 -22 198 -16T137 16T82 83Q39 165 39 320Q39 494 96 585ZM321 597Q291 629 250 629Q208 629 178 597Q153 571 145 525T137 333Q137 175 145 125T181 46Q209 16 250 16Q290 16 318 46Q347 76 354 130T362 333Q362 478 354 524T321 597Z"></path><path id="MJX-2261-TEX-N-2C" d="M78 35T78 60T94 103T137 121Q165 121 187 96T210 8Q210 -27 201 -60T180 -117T154 -158T130 -185T117 -194Q113 -194 104 -185T95 -172Q95 -168 106 -156T131 -126T157 -76T173 -3V9L172 8Q170 7 167 6T161 3T152 1T140 0Q113 0 96 17Z"></path><path id="MJX-2261-TEX-I-1D43E" d="M285 628Q285 635 228 637Q205 637 198 638T191 647Q191 649 193 661Q199 681 203 682Q205 683 214 683H219Q260 681 355 681Q389 681 418 681T463 682T483 682Q500 682 500 674Q500 669 497 660Q496 658 496 654T495 648T493 644T490 641T486 639T479 638T470 637T456 637Q416 636 405 634T387 623L306 305Q307 305 490 449T678 597Q692 611 692 620Q692 635 667 637Q651 637 651 648Q651 650 654 662T659 677Q662 682 676 682Q680 682 711 681T791 680Q814 680 839 681T869 682Q889 682 889 672Q889 650 881 642Q878 637 862 637Q787 632 726 586Q710 576 656 534T556 455L509 418L518 396Q527 374 546 329T581 244Q656 67 661 61Q663 59 666 57Q680 47 717 46H738Q744 38 744 37T741 19Q737 6 731 0H720Q680 3 625 3Q503 3 488 0H478Q472 6 472 9T474 27Q478 40 480 43T491 46H494Q544 46 544 71Q544 75 517 141T485 216L427 354L359 301L291 248L268 155Q245 63 245 58Q245 51 253 49T303 46H334Q340 37 340 35Q340 19 333 5Q328 0 317 0Q314 0 280 1T180 2Q118 2 85 2T49 1Q31 1 31 11Q31 13 34 25Q38 41 42 43T65 46Q92 46 125 49Q139 52 144 61Q147 65 216 339T285 628Z"></path><path id="MJX-2261-TEX-I-1D445" d="M230 637Q203 637 198 638T193 649Q193 676 204 682Q206 683 378 683Q550 682 564 680Q620 672 658 652T712 606T733 563T739 529Q739 484 710 445T643 385T576 351T538 338L545 333Q612 295 612 223Q612 212 607 162T602 80V71Q602 53 603 43T614 25T640 16Q668 16 686 38T712 85Q717 99 720 102T735 105Q755 105 755 93Q755 75 731 36Q693 -21 641 -21H632Q571 -21 531 4T487 82Q487 109 502 166T517 239Q517 290 474 313Q459 320 449 321T378 323H309L277 193Q244 61 244 59Q244 55 245 54T252 50T269 48T302 46H333Q339 38 339 37T336 19Q332 6 326 0H311Q275 2 180 2Q146 2 117 2T71 2T50 1Q33 1 33 10Q33 12 36 24Q41 43 46 45Q50 46 61 46H67Q94 46 127 49Q141 52 146 61Q149 65 218 339T287 628Q287 635 230 637ZM630 554Q630 586 609 608T523 636Q521 636 500 636T462 637H440Q393 637 386 627Q385 624 352 494T319 361Q319 360 388 360Q466 361 492 367Q556 377 592 426Q608 449 619 486T630 554Z"></path><path id="MJX-2261-TEX-N-3D" d="M56 347Q56 360 70 367H707Q722 359 722 347Q722 336 708 328L390 327H72Q56 332 56 347ZM56 153Q56 168 72 173H708Q722 163 722 153Q722 140 707 133H70Q56 140 56 153Z"></path><path id="MJX-2261-TEX-N-31" d="M213 578L200 573Q186 568 160 563T102 556H83V602H102Q149 604 189 617T245 641T273 663Q275 666 285 666Q294 666 302 660V361L303 61Q310 54 315 52T339 48T401 46H427V0H416Q395 3 257 3Q121 3 100 0H88V46H114Q136 46 152 46T177 47T193 50T201 52T207 57T213 61V578Z"></path><path id="MJX-2261-TEX-N-73" d="M295 316Q295 356 268 385T190 414Q154 414 128 401Q98 382 98 349Q97 344 98 336T114 312T157 287Q175 282 201 278T245 269T277 256Q294 248 310 236T342 195T359 133Q359 71 321 31T198 -10H190Q138 -10 94 26L86 19L77 10Q71 4 65 -1L54 -11H46H42Q39 -11 33 -5V74V132Q33 153 35 157T45 162H54Q66 162 70 158T75 146T82 119T101 77Q136 26 198 26Q295 26 295 104Q295 133 277 151Q257 175 194 187T111 210Q75 227 54 256T33 318Q33 357 50 384T93 424T143 442T187 447H198Q238 447 268 432L283 424L292 431Q302 440 314 448H322H326Q329 448 335 442V310L329 304H301Q295 310 295 316Z"></path><path id="MJX-2261-TEX-N-65" d="M28 218Q28 273 48 318T98 391T163 433T229 448Q282 448 320 430T378 380T406 316T415 245Q415 238 408 231H126V216Q126 68 226 36Q246 30 270 30Q312 30 342 62Q359 79 369 104L379 128Q382 131 395 131H398Q415 131 415 121Q415 117 412 108Q393 53 349 21T250 -11Q155 -11 92 58T28 218ZM333 275Q322 403 238 411H236Q228 411 220 410T195 402T166 381T143 340T127 274V267H333V275Z"></path><path id="MJX-2261-TEX-N-63" d="M370 305T349 305T313 320T297 358Q297 381 312 396Q317 401 317 402T307 404Q281 408 258 408Q209 408 178 376Q131 329 131 219Q131 137 162 90Q203 29 272 29Q313 29 338 55T374 117Q376 125 379 127T395 129H409Q415 123 415 120Q415 116 411 104T395 71T366 33T318 2T249 -11Q163 -11 99 53T34 214Q34 318 99 383T250 448T370 421T404 357Q404 334 387 320Z"></path></defs><g stroke="currentColor" fill="currentColor" stroke-width="0" transform="scale(1,-1)"><g data-mml-node="math"><g data-mml-node="msub"><g data-mml-node="mi"><use data-c="1D43A" xlink:href="#MJX-2261-TEX-I-1D43A"></use></g><g data-mml-node="TeXAtom" transform="translate(819,-150) scale(0.707)" data-mjx-texclass="ORD"><g data-mml-node="mn"><use data-c="30" xlink:href="#MJX-2261-TEX-N-30"></use></g><g data-mml-node="mo" transform="translate(500,0)"><use data-c="2C" xlink:href="#MJX-2261-TEX-N-2C"></use></g><g data-mml-node="msub" transform="translate(778,0)"><g data-mml-node="mi"><use data-c="1D43E" xlink:href="#MJX-2261-TEX-I-1D43E"></use></g><g data-mml-node="TeXAtom" transform="translate(882,-150) scale(0.707)" data-mjx-texclass="ORD"><g data-mml-node="mi"><use data-c="1D445" xlink:href="#MJX-2261-TEX-I-1D445"></use></g></g></g><g data-mml-node="mo" transform="translate(2246.7,0)"><use data-c="3D" xlink:href="#MJX-2261-TEX-N-3D"></use></g><g data-mml-node="mn" transform="translate(3024.7,0)"><use data-c="31" xlink:href="#MJX-2261-TEX-N-31"></use></g><g data-mml-node="TeXAtom" data-mjx-texclass="ORD" transform="translate(3524.7,0)"><g data-mml-node="mi"><use data-c="73" xlink:href="#MJX-2261-TEX-N-73"></use><use data-c="65" xlink:href="#MJX-2261-TEX-N-65" transform="translate(394,0)"></use><use data-c="63" xlink:href="#MJX-2261-TEX-N-63" transform="translate(838,0)"></use></g></g></g></g></g></g></svg></mjx-container> besitzt integrierendes Verhalten <mjx-container class="MathJax" jax="SVG"><svg alt=" \left(I T_{2}\right) 
" style="vertical-align: -0.566ex" xmlns="http://www.w3.org/2000/svg" width="5.209ex" height="2.262ex" role="img" focusable="false" viewBox="0 -750 2302.6 1000" xmlns:xlink="http://www.w3.org/1999/xlink"><defs><path id="MJX-2262-TEX-N-28" d="M94 250Q94 319 104 381T127 488T164 576T202 643T244 695T277 729T302 750H315H319Q333 750 333 741Q333 738 316 720T275 667T226 581T184 443T167 250T184 58T225 -81T274 -167T316 -220T333 -241Q333 -250 318 -250H315H302L274 -226Q180 -141 137 -14T94 250Z"></path><path id="MJX-2262-TEX-I-1D43C" d="M43 1Q26 1 26 10Q26 12 29 24Q34 43 39 45Q42 46 54 46H60Q120 46 136 53Q137 53 138 54Q143 56 149 77T198 273Q210 318 216 344Q286 624 286 626Q284 630 284 631Q274 637 213 637H193Q184 643 189 662Q193 677 195 680T209 683H213Q285 681 359 681Q481 681 487 683H497Q504 676 504 672T501 655T494 639Q491 637 471 637Q440 637 407 634Q393 631 388 623Q381 609 337 432Q326 385 315 341Q245 65 245 59Q245 52 255 50T307 46H339Q345 38 345 37T342 19Q338 6 332 0H316Q279 2 179 2Q143 2 113 2T65 2T43 1Z"></path><path id="MJX-2262-TEX-I-1D447" d="M40 437Q21 437 21 445Q21 450 37 501T71 602L88 651Q93 669 101 677H569H659Q691 677 697 676T704 667Q704 661 687 553T668 444Q668 437 649 437Q640 437 637 437T631 442L629 445Q629 451 635 490T641 551Q641 586 628 604T573 629Q568 630 515 631Q469 631 457 630T439 622Q438 621 368 343T298 60Q298 48 386 46Q418 46 427 45T436 36Q436 31 433 22Q429 4 424 1L422 0Q419 0 415 0Q410 0 363 1T228 2Q99 2 64 0H49Q43 6 43 9T45 27Q49 40 55 46H83H94Q174 46 189 55Q190 56 191 56Q196 59 201 76T241 233Q258 301 269 344Q339 619 339 625Q339 630 310 630H279Q212 630 191 624Q146 614 121 583T67 467Q60 445 57 441T43 437H40Z"></path><path id="MJX-2262-TEX-N-32" d="M109 429Q82 429 66 447T50 491Q50 562 103 614T235 666Q326 666 387 610T449 465Q449 422 429 383T381 315T301 241Q265 210 201 149L142 93L218 92Q375 92 385 97Q392 99 409 186V189H449V186Q448 183 436 95T421 3V0H50V19V31Q50 38 56 46T86 81Q115 113 136 137Q145 147 170 174T204 211T233 244T261 278T284 308T305 340T320 369T333 401T340 431T343 464Q343 527 309 573T212 619Q179 619 154 602T119 569T109 550Q109 549 114 549Q132 549 151 535T170 489Q170 464 154 447T109 429Z"></path><path id="MJX-2262-TEX-N-29" d="M60 749L64 750Q69 750 74 750H86L114 726Q208 641 251 514T294 250Q294 182 284 119T261 12T224 -76T186 -143T145 -194T113 -227T90 -246Q87 -249 86 -250H74Q66 -250 63 -250T58 -247T55 -238Q56 -237 66 -225Q221 -64 221 250T66 725Q56 737 55 738Q55 746 60 749Z"></path></defs><g stroke="currentColor" fill="currentColor" stroke-width="0" transform="scale(1,-1)"><g data-mml-node="math"><g data-mml-node="mrow"><g data-mml-node="mo"><use data-c="28" xlink:href="#MJX-2262-TEX-N-28"></use></g><g data-mml-node="mi" transform="translate(389,0)"><use data-c="1D43C" xlink:href="#MJX-2262-TEX-I-1D43C"></use></g><g data-mml-node="msub" transform="translate(893,0)"><g data-mml-node="mi"><use data-c="1D447" xlink:href="#MJX-2262-TEX-I-1D447"></use></g><g data-mml-node="TeXAtom" transform="translate(617,-150) scale(0.707)" data-mjx-texclass="ORD"><g data-mml-node="mn"><use data-c="32" xlink:href="#MJX-2262-TEX-N-32"></use></g></g></g><g data-mml-node="mo" transform="translate(1913.6,0)"><use data-c="29" xlink:href="#MJX-2262-TEX-N-29"></use></g></g></g></g></svg></mjx-container></p>


<p>\( \varphi_{0, K_{R}=1 \mathrm{sec}} \) schneidet \( -180^{\circ} \) nur mit negativer Steigung</p>


<p><mjx-container class="MathJax" jax="SVG"><svg alt=" \varphi_{0, K_{R}=1 \mathrm{sec}} " style="vertical-align: -0.65ex" xmlns="http://www.w3.org/2000/svg" width="9.357ex" height="1.65ex" role="img" focusable="false" viewBox="0 -442 4135.8 729.2" xmlns:xlink="http://www.w3.org/1999/xlink"><defs><path id="MJX-2263-TEX-I-1D711" d="M92 210Q92 176 106 149T142 108T185 85T220 72L235 70L237 71L250 112Q268 170 283 211T322 299T370 375T429 423T502 442Q547 442 582 410T618 302Q618 224 575 152T457 35T299 -10Q273 -10 273 -12L266 -48Q260 -83 252 -125T241 -179Q236 -203 215 -212Q204 -218 190 -218Q159 -215 159 -185Q159 -175 214 -2L209 0Q204 2 195 5T173 14T147 28T120 46T94 71T71 103T56 142T50 190Q50 238 76 311T149 431H162Q183 431 183 423Q183 417 175 409Q134 361 114 300T92 210ZM574 278Q574 320 550 344T486 369Q437 369 394 329T323 218Q309 184 295 109L286 64Q304 62 306 62Q423 62 498 131T574 278Z"></path><path id="MJX-2263-TEX-N-30" d="M96 585Q152 666 249 666Q297 666 345 640T423 548Q460 465 460 320Q460 165 417 83Q397 41 362 16T301 -15T250 -22Q224 -22 198 -16T137 16T82 83Q39 165 39 320Q39 494 96 585ZM321 597Q291 629 250 629Q208 629 178 597Q153 571 145 525T137 333Q137 175 145 125T181 46Q209 16 250 16Q290 16 318 46Q347 76 354 130T362 333Q362 478 354 524T321 597Z"></path><path id="MJX-2263-TEX-N-2C" d="M78 35T78 60T94 103T137 121Q165 121 187 96T210 8Q210 -27 201 -60T180 -117T154 -158T130 -185T117 -194Q113 -194 104 -185T95 -172Q95 -168 106 -156T131 -126T157 -76T173 -3V9L172 8Q170 7 167 6T161 3T152 1T140 0Q113 0 96 17Z"></path><path id="MJX-2263-TEX-I-1D43E" d="M285 628Q285 635 228 637Q205 637 198 638T191 647Q191 649 193 661Q199 681 203 682Q205 683 214 683H219Q260 681 355 681Q389 681 418 681T463 682T483 682Q500 682 500 674Q500 669 497 660Q496 658 496 654T495 648T493 644T490 641T486 639T479 638T470 637T456 637Q416 636 405 634T387 623L306 305Q307 305 490 449T678 597Q692 611 692 620Q692 635 667 637Q651 637 651 648Q651 650 654 662T659 677Q662 682 676 682Q680 682 711 681T791 680Q814 680 839 681T869 682Q889 682 889 672Q889 650 881 642Q878 637 862 637Q787 632 726 586Q710 576 656 534T556 455L509 418L518 396Q527 374 546 329T581 244Q656 67 661 61Q663 59 666 57Q680 47 717 46H738Q744 38 744 37T741 19Q737 6 731 0H720Q680 3 625 3Q503 3 488 0H478Q472 6 472 9T474 27Q478 40 480 43T491 46H494Q544 46 544 71Q544 75 517 141T485 216L427 354L359 301L291 248L268 155Q245 63 245 58Q245 51 253 49T303 46H334Q340 37 340 35Q340 19 333 5Q328 0 317 0Q314 0 280 1T180 2Q118 2 85 2T49 1Q31 1 31 11Q31 13 34 25Q38 41 42 43T65 46Q92 46 125 49Q139 52 144 61Q147 65 216 339T285 628Z"></path><path id="MJX-2263-TEX-I-1D445" d="M230 637Q203 637 198 638T193 649Q193 676 204 682Q206 683 378 683Q550 682 564 680Q620 672 658 652T712 606T733 563T739 529Q739 484 710 445T643 385T576 351T538 338L545 333Q612 295 612 223Q612 212 607 162T602 80V71Q602 53 603 43T614 25T640 16Q668 16 686 38T712 85Q717 99 720 102T735 105Q755 105 755 93Q755 75 731 36Q693 -21 641 -21H632Q571 -21 531 4T487 82Q487 109 502 166T517 239Q517 290 474 313Q459 320 449 321T378 323H309L277 193Q244 61 244 59Q244 55 245 54T252 50T269 48T302 46H333Q339 38 339 37T336 19Q332 6 326 0H311Q275 2 180 2Q146 2 117 2T71 2T50 1Q33 1 33 10Q33 12 36 24Q41 43 46 45Q50 46 61 46H67Q94 46 127 49Q141 52 146 61Q149 65 218 339T287 628Q287 635 230 637ZM630 554Q630 586 609 608T523 636Q521 636 500 636T462 637H440Q393 637 386 627Q385 624 352 494T319 361Q319 360 388 360Q466 361 492 367Q556 377 592 426Q608 449 619 486T630 554Z"></path><path id="MJX-2263-TEX-N-3D" d="M56 347Q56 360 70 367H707Q722 359 722 347Q722 336 708 328L390 327H72Q56 332 56 347ZM56 153Q56 168 72 173H708Q722 163 722 153Q722 140 707 133H70Q56 140 56 153Z"></path><path id="MJX-2263-TEX-N-31" d="M213 578L200 573Q186 568 160 563T102 556H83V602H102Q149 604 189 617T245 641T273 663Q275 666 285 666Q294 666 302 660V361L303 61Q310 54 315 52T339 48T401 46H427V0H416Q395 3 257 3Q121 3 100 0H88V46H114Q136 46 152 46T177 47T193 50T201 52T207 57T213 61V578Z"></path><path id="MJX-2263-TEX-N-73" d="M295 316Q295 356 268 385T190 414Q154 414 128 401Q98 382 98 349Q97 344 98 336T114 312T157 287Q175 282 201 278T245 269T277 256Q294 248 310 236T342 195T359 133Q359 71 321 31T198 -10H190Q138 -10 94 26L86 19L77 10Q71 4 65 -1L54 -11H46H42Q39 -11 33 -5V74V132Q33 153 35 157T45 162H54Q66 162 70 158T75 146T82 119T101 77Q136 26 198 26Q295 26 295 104Q295 133 277 151Q257 175 194 187T111 210Q75 227 54 256T33 318Q33 357 50 384T93 424T143 442T187 447H198Q238 447 268 432L283 424L292 431Q302 440 314 448H322H326Q329 448 335 442V310L329 304H301Q295 310 295 316Z"></path><path id="MJX-2263-TEX-N-65" d="M28 218Q28 273 48 318T98 391T163 433T229 448Q282 448 320 430T378 380T406 316T415 245Q415 238 408 231H126V216Q126 68 226 36Q246 30 270 30Q312 30 342 62Q359 79 369 104L379 128Q382 131 395 131H398Q415 131 415 121Q415 117 412 108Q393 53 349 21T250 -11Q155 -11 92 58T28 218ZM333 275Q322 403 238 411H236Q228 411 220 410T195 402T166 381T143 340T127 274V267H333V275Z"></path><path id="MJX-2263-TEX-N-63" d="M370 305T349 305T313 320T297 358Q297 381 312 396Q317 401 317 402T307 404Q281 408 258 408Q209 408 178 376Q131 329 131 219Q131 137 162 90Q203 29 272 29Q313 29 338 55T374 117Q376 125 379 127T395 129H409Q415 123 415 120Q415 116 411 104T395 71T366 33T318 2T249 -11Q163 -11 99 53T34 214Q34 318 99 383T250 448T370 421T404 357Q404 334 387 320Z"></path></defs><g stroke="currentColor" fill="currentColor" stroke-width="0" transform="scale(1,-1)"><g data-mml-node="math"><g data-mml-node="msub"><g data-mml-node="mi"><use data-c="1D711" xlink:href="#MJX-2263-TEX-I-1D711"></use></g><g data-mml-node="TeXAtom" transform="translate(687,-150) scale(0.707)" data-mjx-texclass="ORD"><g data-mml-node="mn"><use data-c="30" xlink:href="#MJX-2263-TEX-N-30"></use></g><g data-mml-node="mo" transform="translate(500,0)"><use data-c="2C" xlink:href="#MJX-2263-TEX-N-2C"></use></g><g data-mml-node="msub" transform="translate(778,0)"><g data-mml-node="mi"><use data-c="1D43E" xlink:href="#MJX-2263-TEX-I-1D43E"></use></g><g data-mml-node="TeXAtom" transform="translate(882,-150) scale(0.707)" data-mjx-texclass="ORD"><g data-mml-node="mi"><use data-c="1D445" xlink:href="#MJX-2263-TEX-I-1D445"></use></g></g></g><g data-mml-node="mo" transform="translate(2246.7,0)"><use data-c="3D" xlink:href="#MJX-2263-TEX-N-3D"></use></g><g data-mml-node="mn" transform="translate(3024.7,0)"><use data-c="31" xlink:href="#MJX-2263-TEX-N-31"></use></g><g data-mml-node="TeXAtom" data-mjx-texclass="ORD" transform="translate(3524.7,0)"><g data-mml-node="mi"><use data-c="73" xlink:href="#MJX-2263-TEX-N-73"></use><use data-c="65" xlink:href="#MJX-2263-TEX-N-65" transform="translate(394,0)"></use><use data-c="63" xlink:href="#MJX-2263-TEX-N-63" transform="translate(838,0)"></use></g></g></g></g></g></g></svg></mjx-container> schneidet <mjx-container class="MathJax" jax="SVG"><svg alt=" -180^{\circ} " style="vertical-align: -0.186ex" xmlns="http://www.w3.org/2000/svg" width="6.142ex" height="1.785ex" role="img" focusable="false" viewBox="0 -707 2714.6 789" xmlns:xlink="http://www.w3.org/1999/xlink"><defs><path id="MJX-2264-TEX-N-2212" d="M84 237T84 250T98 270H679Q694 262 694 250T679 230H98Q84 237 84 250Z"></path><path id="MJX-2264-TEX-N-31" d="M213 578L200 573Q186 568 160 563T102 556H83V602H102Q149 604 189 617T245 641T273 663Q275 666 285 666Q294 666 302 660V361L303 61Q310 54 315 52T339 48T401 46H427V0H416Q395 3 257 3Q121 3 100 0H88V46H114Q136 46 152 46T177 47T193 50T201 52T207 57T213 61V578Z"></path><path id="MJX-2264-TEX-N-38" d="M70 417T70 494T124 618T248 666Q319 666 374 624T429 515Q429 485 418 459T392 417T361 389T335 371T324 363L338 354Q352 344 366 334T382 323Q457 264 457 174Q457 95 399 37T249 -22Q159 -22 101 29T43 155Q43 263 172 335L154 348Q133 361 127 368Q70 417 70 494ZM286 386L292 390Q298 394 301 396T311 403T323 413T334 425T345 438T355 454T364 471T369 491T371 513Q371 556 342 586T275 624Q268 625 242 625Q201 625 165 599T128 534Q128 511 141 492T167 463T217 431Q224 426 228 424L286 386ZM250 21Q308 21 350 55T392 137Q392 154 387 169T375 194T353 216T330 234T301 253T274 270Q260 279 244 289T218 306L210 311Q204 311 181 294T133 239T107 157Q107 98 150 60T250 21Z"></path><path id="MJX-2264-TEX-N-30" d="M96 585Q152 666 249 666Q297 666 345 640T423 548Q460 465 460 320Q460 165 417 83Q397 41 362 16T301 -15T250 -22Q224 -22 198 -16T137 16T82 83Q39 165 39 320Q39 494 96 585ZM321 597Q291 629 250 629Q208 629 178 597Q153 571 145 525T137 333Q137 175 145 125T181 46Q209 16 250 16Q290 16 318 46Q347 76 354 130T362 333Q362 478 354 524T321 597Z"></path><path id="MJX-2264-TEX-N-2218" d="M55 251Q55 328 112 386T249 444T386 388T444 249Q444 171 388 113T250 55Q170 55 113 112T55 251ZM245 403Q188 403 142 361T96 250Q96 183 141 140T250 96Q284 96 313 109T354 135T375 160Q403 197 403 250Q403 313 360 358T245 403Z"></path></defs><g stroke="currentColor" fill="currentColor" stroke-width="0" transform="scale(1,-1)"><g data-mml-node="math"><g data-mml-node="mo"><use data-c="2212" xlink:href="#MJX-2264-TEX-N-2212"></use></g><g data-mml-node="msup" transform="translate(778,0)"><g data-mml-node="mn"><use data-c="31" xlink:href="#MJX-2264-TEX-N-31"></use><use data-c="38" xlink:href="#MJX-2264-TEX-N-38" transform="translate(500,0)"></use><use data-c="30" xlink:href="#MJX-2264-TEX-N-30" transform="translate(1000,0)"></use></g><g data-mml-node="TeXAtom" transform="translate(1533,393.1) scale(0.707)" data-mjx-texclass="ORD"><g data-mml-node="mo"><use data-c="2218" xlink:href="#MJX-2264-TEX-N-2218"></use></g></g></g></g></g></svg></mjx-container> nur mit negativer Steigung</p>


<p>Das vereinfachte Nyquist-Kriterium ist anwendbar.</p>


<p>\[<br />\left|G_{0, K_{R}=1 \sec }\left(j \omega_{\pi}\right)\right| &gt; 1 <br />\]</p>


<p><mjx-container class="MathJax" jax="SVG" display="true" justify="left"><svg alt="
\left|G_{0, K_{R}=1 \sec }\left(j \omega_{\pi}\right)\right| > 1 
" style="vertical-align: -0.65ex" xmlns="http://www.w3.org/2000/svg" width="20.905ex" height="2.347ex" role="img" focusable="false" viewBox="0 -750 9240 1037.2" xmlns:xlink="http://www.w3.org/1999/xlink"><defs><path id="MJX-2265-TEX-N-7C" d="M139 -249H137Q125 -249 119 -235V251L120 737Q130 750 139 750Q152 750 159 735V-235Q151 -249 141 -249H139Z"></path><path id="MJX-2265-TEX-I-1D43A" d="M50 252Q50 367 117 473T286 641T490 704Q580 704 633 653Q642 643 648 636T656 626L657 623Q660 623 684 649Q691 655 699 663T715 679T725 690L740 705H746Q760 705 760 698Q760 694 728 561Q692 422 692 421Q690 416 687 415T669 413H653Q647 419 647 422Q647 423 648 429T650 449T651 481Q651 552 619 605T510 659Q492 659 471 656T418 643T357 615T294 567T236 496T189 394T158 260Q156 242 156 221Q156 173 170 136T206 79T256 45T308 28T353 24Q407 24 452 47T514 106Q517 114 529 161T541 214Q541 222 528 224T468 227H431Q425 233 425 235T427 254Q431 267 437 273H454Q494 271 594 271Q634 271 659 271T695 272T707 272Q721 272 721 263Q721 261 719 249Q714 230 709 228Q706 227 694 227Q674 227 653 224Q646 221 643 215T629 164Q620 131 614 108Q589 6 586 3Q584 1 581 1Q571 1 553 21T530 52Q530 53 528 52T522 47Q448 -22 322 -22Q201 -22 126 55T50 252Z"></path><path id="MJX-2265-TEX-N-30" d="M96 585Q152 666 249 666Q297 666 345 640T423 548Q460 465 460 320Q460 165 417 83Q397 41 362 16T301 -15T250 -22Q224 -22 198 -16T137 16T82 83Q39 165 39 320Q39 494 96 585ZM321 597Q291 629 250 629Q208 629 178 597Q153 571 145 525T137 333Q137 175 145 125T181 46Q209 16 250 16Q290 16 318 46Q347 76 354 130T362 333Q362 478 354 524T321 597Z"></path><path id="MJX-2265-TEX-N-2C" d="M78 35T78 60T94 103T137 121Q165 121 187 96T210 8Q210 -27 201 -60T180 -117T154 -158T130 -185T117 -194Q113 -194 104 -185T95 -172Q95 -168 106 -156T131 -126T157 -76T173 -3V9L172 8Q170 7 167 6T161 3T152 1T140 0Q113 0 96 17Z"></path><path id="MJX-2265-TEX-I-1D43E" d="M285 628Q285 635 228 637Q205 637 198 638T191 647Q191 649 193 661Q199 681 203 682Q205 683 214 683H219Q260 681 355 681Q389 681 418 681T463 682T483 682Q500 682 500 674Q500 669 497 660Q496 658 496 654T495 648T493 644T490 641T486 639T479 638T470 637T456 637Q416 636 405 634T387 623L306 305Q307 305 490 449T678 597Q692 611 692 620Q692 635 667 637Q651 637 651 648Q651 650 654 662T659 677Q662 682 676 682Q680 682 711 681T791 680Q814 680 839 681T869 682Q889 682 889 672Q889 650 881 642Q878 637 862 637Q787 632 726 586Q710 576 656 534T556 455L509 418L518 396Q527 374 546 329T581 244Q656 67 661 61Q663 59 666 57Q680 47 717 46H738Q744 38 744 37T741 19Q737 6 731 0H720Q680 3 625 3Q503 3 488 0H478Q472 6 472 9T474 27Q478 40 480 43T491 46H494Q544 46 544 71Q544 75 517 141T485 216L427 354L359 301L291 248L268 155Q245 63 245 58Q245 51 253 49T303 46H334Q340 37 340 35Q340 19 333 5Q328 0 317 0Q314 0 280 1T180 2Q118 2 85 2T49 1Q31 1 31 11Q31 13 34 25Q38 41 42 43T65 46Q92 46 125 49Q139 52 144 61Q147 65 216 339T285 628Z"></path><path id="MJX-2265-TEX-I-1D445" d="M230 637Q203 637 198 638T193 649Q193 676 204 682Q206 683 378 683Q550 682 564 680Q620 672 658 652T712 606T733 563T739 529Q739 484 710 445T643 385T576 351T538 338L545 333Q612 295 612 223Q612 212 607 162T602 80V71Q602 53 603 43T614 25T640 16Q668 16 686 38T712 85Q717 99 720 102T735 105Q755 105 755 93Q755 75 731 36Q693 -21 641 -21H632Q571 -21 531 4T487 82Q487 109 502 166T517 239Q517 290 474 313Q459 320 449 321T378 323H309L277 193Q244 61 244 59Q244 55 245 54T252 50T269 48T302 46H333Q339 38 339 37T336 19Q332 6 326 0H311Q275 2 180 2Q146 2 117 2T71 2T50 1Q33 1 33 10Q33 12 36 24Q41 43 46 45Q50 46 61 46H67Q94 46 127 49Q141 52 146 61Q149 65 218 339T287 628Q287 635 230 637ZM630 554Q630 586 609 608T523 636Q521 636 500 636T462 637H440Q393 637 386 627Q385 624 352 494T319 361Q319 360 388 360Q466 361 492 367Q556 377 592 426Q608 449 619 486T630 554Z"></path><path id="MJX-2265-TEX-N-3D" d="M56 347Q56 360 70 367H707Q722 359 722 347Q722 336 708 328L390 327H72Q56 332 56 347ZM56 153Q56 168 72 173H708Q722 163 722 153Q722 140 707 133H70Q56 140 56 153Z"></path><path id="MJX-2265-TEX-N-31" d="M213 578L200 573Q186 568 160 563T102 556H83V602H102Q149 604 189 617T245 641T273 663Q275 666 285 666Q294 666 302 660V361L303 61Q310 54 315 52T339 48T401 46H427V0H416Q395 3 257 3Q121 3 100 0H88V46H114Q136 46 152 46T177 47T193 50T201 52T207 57T213 61V578Z"></path><path id="MJX-2265-TEX-N-73" d="M295 316Q295 356 268 385T190 414Q154 414 128 401Q98 382 98 349Q97 344 98 336T114 312T157 287Q175 282 201 278T245 269T277 256Q294 248 310 236T342 195T359 133Q359 71 321 31T198 -10H190Q138 -10 94 26L86 19L77 10Q71 4 65 -1L54 -11H46H42Q39 -11 33 -5V74V132Q33 153 35 157T45 162H54Q66 162 70 158T75 146T82 119T101 77Q136 26 198 26Q295 26 295 104Q295 133 277 151Q257 175 194 187T111 210Q75 227 54 256T33 318Q33 357 50 384T93 424T143 442T187 447H198Q238 447 268 432L283 424L292 431Q302 440 314 448H322H326Q329 448 335 442V310L329 304H301Q295 310 295 316Z"></path><path id="MJX-2265-TEX-N-65" d="M28 218Q28 273 48 318T98 391T163 433T229 448Q282 448 320 430T378 380T406 316T415 245Q415 238 408 231H126V216Q126 68 226 36Q246 30 270 30Q312 30 342 62Q359 79 369 104L379 128Q382 131 395 131H398Q415 131 415 121Q415 117 412 108Q393 53 349 21T250 -11Q155 -11 92 58T28 218ZM333 275Q322 403 238 411H236Q228 411 220 410T195 402T166 381T143 340T127 274V267H333V275Z"></path><path id="MJX-2265-TEX-N-63" d="M370 305T349 305T313 320T297 358Q297 381 312 396Q317 401 317 402T307 404Q281 408 258 408Q209 408 178 376Q131 329 131 219Q131 137 162 90Q203 29 272 29Q313 29 338 55T374 117Q376 125 379 127T395 129H409Q415 123 415 120Q415 116 411 104T395 71T366 33T318 2T249 -11Q163 -11 99 53T34 214Q34 318 99 383T250 448T370 421T404 357Q404 334 387 320Z"></path><path id="MJX-2265-TEX-N-28" d="M94 250Q94 319 104 381T127 488T164 576T202 643T244 695T277 729T302 750H315H319Q333 750 333 741Q333 738 316 720T275 667T226 581T184 443T167 250T184 58T225 -81T274 -167T316 -220T333 -241Q333 -250 318 -250H315H302L274 -226Q180 -141 137 -14T94 250Z"></path><path id="MJX-2265-TEX-I-1D457" d="M297 596Q297 627 318 644T361 661Q378 661 389 651T403 623Q403 595 384 576T340 557Q322 557 310 567T297 596ZM288 376Q288 405 262 405Q240 405 220 393T185 362T161 325T144 293L137 279Q135 278 121 278H107Q101 284 101 286T105 299Q126 348 164 391T252 441Q253 441 260 441T272 442Q296 441 316 432Q341 418 354 401T367 348V332L318 133Q267 -67 264 -75Q246 -125 194 -164T75 -204Q25 -204 7 -183T-12 -137Q-12 -110 7 -91T53 -71Q70 -71 82 -81T95 -112Q95 -148 63 -167Q69 -168 77 -168Q111 -168 139 -140T182 -74L193 -32Q204 11 219 72T251 197T278 308T289 365Q289 372 288 376Z"></path><path id="MJX-2265-TEX-I-1D714" d="M495 384Q495 406 514 424T555 443Q574 443 589 425T604 364Q604 334 592 278T555 155T483 38T377 -11Q297 -11 267 66Q266 68 260 61Q201 -11 125 -11Q15 -11 15 139Q15 230 56 325T123 434Q135 441 147 436Q160 429 160 418Q160 406 140 379T94 306T62 208Q61 202 61 187Q61 124 85 100T143 76Q201 76 245 129L253 137V156Q258 297 317 297Q348 297 348 261Q348 243 338 213T318 158L308 135Q309 133 310 129T318 115T334 97T358 83T393 76Q456 76 501 148T546 274Q546 305 533 325T508 357T495 384Z"></path><path id="MJX-2265-TEX-I-1D70B" d="M132 -11Q98 -11 98 22V33L111 61Q186 219 220 334L228 358H196Q158 358 142 355T103 336Q92 329 81 318T62 297T53 285Q51 284 38 284Q19 284 19 294Q19 300 38 329T93 391T164 429Q171 431 389 431Q549 431 553 430Q573 423 573 402Q573 371 541 360Q535 358 472 358H408L405 341Q393 269 393 222Q393 170 402 129T421 65T431 37Q431 20 417 5T381 -10Q370 -10 363 -7T347 17T331 77Q330 86 330 121Q330 170 339 226T357 318T367 358H269L268 354Q268 351 249 275T206 114T175 17Q164 -11 132 -11Z"></path><path id="MJX-2265-TEX-N-29" d="M60 749L64 750Q69 750 74 750H86L114 726Q208 641 251 514T294 250Q294 182 284 119T261 12T224 -76T186 -143T145 -194T113 -227T90 -246Q87 -249 86 -250H74Q66 -250 63 -250T58 -247T55 -238Q56 -237 66 -225Q221 -64 221 250T66 725Q56 737 55 738Q55 746 60 749Z"></path><path id="MJX-2265-TEX-N-3E" d="M84 520Q84 528 88 533T96 539L99 540Q106 540 253 471T544 334L687 265Q694 260 694 250T687 235Q685 233 395 96L107 -40H101Q83 -38 83 -20Q83 -19 83 -17Q82 -10 98 -1Q117 9 248 71Q326 108 378 132L626 250L378 368Q90 504 86 509Q84 513 84 520Z"></path></defs><g stroke="currentColor" fill="currentColor" stroke-width="0" transform="scale(1,-1)"><g data-mml-node="math"><g data-mml-node="mrow"><g data-mml-node="mo" transform="translate(0 -0.5)"><use data-c="7C" xlink:href="#MJX-2265-TEX-N-7C"></use></g><g data-mml-node="msub" transform="translate(278,0)"><g data-mml-node="mi"><use data-c="1D43A" xlink:href="#MJX-2265-TEX-I-1D43A"></use></g><g data-mml-node="TeXAtom" transform="translate(819,-150) scale(0.707)" data-mjx-texclass="ORD"><g data-mml-node="mn"><use data-c="30" xlink:href="#MJX-2265-TEX-N-30"></use></g><g data-mml-node="mo" transform="translate(500,0)"><use data-c="2C" xlink:href="#MJX-2265-TEX-N-2C"></use></g><g data-mml-node="msub" transform="translate(778,0)"><g data-mml-node="mi"><use data-c="1D43E" xlink:href="#MJX-2265-TEX-I-1D43E"></use></g><g data-mml-node="TeXAtom" transform="translate(882,-150) scale(0.707)" data-mjx-texclass="ORD"><g data-mml-node="mi"><use data-c="1D445" xlink:href="#MJX-2265-TEX-I-1D445"></use></g></g></g><g data-mml-node="mo" transform="translate(2246.7,0)"><use data-c="3D" xlink:href="#MJX-2265-TEX-N-3D"></use></g><g data-mml-node="mn" transform="translate(3024.7,0)"><use data-c="31" xlink:href="#MJX-2265-TEX-N-31"></use></g><g data-mml-node="mi" transform="translate(3691.4,0)"><use data-c="73" xlink:href="#MJX-2265-TEX-N-73"></use><use data-c="65" xlink:href="#MJX-2265-TEX-N-65" transform="translate(394,0)"></use><use data-c="63" xlink:href="#MJX-2265-TEX-N-63" transform="translate(838,0)"></use></g></g></g><g data-mml-node="mrow" transform="translate(4830.4,0)"><g data-mml-node="mo"><use data-c="28" xlink:href="#MJX-2265-TEX-N-28"></use></g><g data-mml-node="mi" transform="translate(389,0)"><use data-c="1D457" xlink:href="#MJX-2265-TEX-I-1D457"></use></g><g data-mml-node="msub" transform="translate(801,0)"><g data-mml-node="mi"><use data-c="1D714" xlink:href="#MJX-2265-TEX-I-1D714"></use></g><g data-mml-node="TeXAtom" transform="translate(655,-150) scale(0.707)" data-mjx-texclass="ORD"><g data-mml-node="mi"><use data-c="1D70B" xlink:href="#MJX-2265-TEX-I-1D70B"></use></g></g></g><g data-mml-node="mo" transform="translate(1909.1,0)"><use data-c="29" xlink:href="#MJX-2265-TEX-N-29"></use></g></g><g data-mml-node="mo" transform="translate(7128.4,0) translate(0 -0.5)"><use data-c="7C" xlink:href="#MJX-2265-TEX-N-7C"></use></g></g><g data-mml-node="mo" transform="translate(7684.2,0)"><use data-c="3E" xlink:href="#MJX-2265-TEX-N-3E"></use></g><g data-mml-node="mn" transform="translate(8740,0)"><use data-c="31" xlink:href="#MJX-2265-TEX-N-31"></use></g></g></g></svg></mjx-container></p>


<p>Der geschlossene Regelkreis ist für \( K_{R}=1 \ sec\) instabil.</p>


<p>Der geschlossene Regelkreis ist für <mjx-container class="MathJax" jax="SVG"><svg alt=" K_{R}=1 \ sec" style="vertical-align: -0.373ex" xmlns="http://www.w3.org/2000/svg" width="11.132ex" height="1.918ex" role="img" focusable="false" viewBox="0 -683 4920.2 847.8" xmlns:xlink="http://www.w3.org/1999/xlink"><defs><path id="MJX-2266-TEX-I-1D43E" d="M285 628Q285 635 228 637Q205 637 198 638T191 647Q191 649 193 661Q199 681 203 682Q205 683 214 683H219Q260 681 355 681Q389 681 418 681T463 682T483 682Q500 682 500 674Q500 669 497 660Q496 658 496 654T495 648T493 644T490 641T486 639T479 638T470 637T456 637Q416 636 405 634T387 623L306 305Q307 305 490 449T678 597Q692 611 692 620Q692 635 667 637Q651 637 651 648Q651 650 654 662T659 677Q662 682 676 682Q680 682 711 681T791 680Q814 680 839 681T869 682Q889 682 889 672Q889 650 881 642Q878 637 862 637Q787 632 726 586Q710 576 656 534T556 455L509 418L518 396Q527 374 546 329T581 244Q656 67 661 61Q663 59 666 57Q680 47 717 46H738Q744 38 744 37T741 19Q737 6 731 0H720Q680 3 625 3Q503 3 488 0H478Q472 6 472 9T474 27Q478 40 480 43T491 46H494Q544 46 544 71Q544 75 517 141T485 216L427 354L359 301L291 248L268 155Q245 63 245 58Q245 51 253 49T303 46H334Q340 37 340 35Q340 19 333 5Q328 0 317 0Q314 0 280 1T180 2Q118 2 85 2T49 1Q31 1 31 11Q31 13 34 25Q38 41 42 43T65 46Q92 46 125 49Q139 52 144 61Q147 65 216 339T285 628Z"></path><path id="MJX-2266-TEX-I-1D445" d="M230 637Q203 637 198 638T193 649Q193 676 204 682Q206 683 378 683Q550 682 564 680Q620 672 658 652T712 606T733 563T739 529Q739 484 710 445T643 385T576 351T538 338L545 333Q612 295 612 223Q612 212 607 162T602 80V71Q602 53 603 43T614 25T640 16Q668 16 686 38T712 85Q717 99 720 102T735 105Q755 105 755 93Q755 75 731 36Q693 -21 641 -21H632Q571 -21 531 4T487 82Q487 109 502 166T517 239Q517 290 474 313Q459 320 449 321T378 323H309L277 193Q244 61 244 59Q244 55 245 54T252 50T269 48T302 46H333Q339 38 339 37T336 19Q332 6 326 0H311Q275 2 180 2Q146 2 117 2T71 2T50 1Q33 1 33 10Q33 12 36 24Q41 43 46 45Q50 46 61 46H67Q94 46 127 49Q141 52 146 61Q149 65 218 339T287 628Q287 635 230 637ZM630 554Q630 586 609 608T523 636Q521 636 500 636T462 637H440Q393 637 386 627Q385 624 352 494T319 361Q319 360 388 360Q466 361 492 367Q556 377 592 426Q608 449 619 486T630 554Z"></path><path id="MJX-2266-TEX-N-3D" d="M56 347Q56 360 70 367H707Q722 359 722 347Q722 336 708 328L390 327H72Q56 332 56 347ZM56 153Q56 168 72 173H708Q722 163 722 153Q722 140 707 133H70Q56 140 56 153Z"></path><path id="MJX-2266-TEX-N-31" d="M213 578L200 573Q186 568 160 563T102 556H83V602H102Q149 604 189 617T245 641T273 663Q275 666 285 666Q294 666 302 660V361L303 61Q310 54 315 52T339 48T401 46H427V0H416Q395 3 257 3Q121 3 100 0H88V46H114Q136 46 152 46T177 47T193 50T201 52T207 57T213 61V578Z"></path><path id="MJX-2266-TEX-N-A0" d=""></path><path id="MJX-2266-TEX-I-1D460" d="M131 289Q131 321 147 354T203 415T300 442Q362 442 390 415T419 355Q419 323 402 308T364 292Q351 292 340 300T328 326Q328 342 337 354T354 372T367 378Q368 378 368 379Q368 382 361 388T336 399T297 405Q249 405 227 379T204 326Q204 301 223 291T278 274T330 259Q396 230 396 163Q396 135 385 107T352 51T289 7T195 -10Q118 -10 86 19T53 87Q53 126 74 143T118 160Q133 160 146 151T160 120Q160 94 142 76T111 58Q109 57 108 57T107 55Q108 52 115 47T146 34T201 27Q237 27 263 38T301 66T318 97T323 122Q323 150 302 164T254 181T195 196T148 231Q131 256 131 289Z"></path><path id="MJX-2266-TEX-I-1D452" d="M39 168Q39 225 58 272T107 350T174 402T244 433T307 442H310Q355 442 388 420T421 355Q421 265 310 237Q261 224 176 223Q139 223 138 221Q138 219 132 186T125 128Q125 81 146 54T209 26T302 45T394 111Q403 121 406 121Q410 121 419 112T429 98T420 82T390 55T344 24T281 -1T205 -11Q126 -11 83 42T39 168ZM373 353Q367 405 305 405Q272 405 244 391T199 357T170 316T154 280T149 261Q149 260 169 260Q282 260 327 284T373 353Z"></path><path id="MJX-2266-TEX-I-1D450" d="M34 159Q34 268 120 355T306 442Q362 442 394 418T427 355Q427 326 408 306T360 285Q341 285 330 295T319 325T330 359T352 380T366 386H367Q367 388 361 392T340 400T306 404Q276 404 249 390Q228 381 206 359Q162 315 142 235T121 119Q121 73 147 50Q169 26 205 26H209Q321 26 394 111Q403 121 406 121Q410 121 419 112T429 98T420 83T391 55T346 25T282 0T202 -11Q127 -11 81 37T34 159Z"></path></defs><g stroke="currentColor" fill="currentColor" stroke-width="0" transform="scale(1,-1)"><g data-mml-node="math"><g data-mml-node="msub"><g data-mml-node="mi"><use data-c="1D43E" xlink:href="#MJX-2266-TEX-I-1D43E"></use></g><g data-mml-node="TeXAtom" transform="translate(882,-150) scale(0.707)" data-mjx-texclass="ORD"><g data-mml-node="mi"><use data-c="1D445" xlink:href="#MJX-2266-TEX-I-1D445"></use></g></g></g><g data-mml-node="mo" transform="translate(1746.5,0)"><use data-c="3D" xlink:href="#MJX-2266-TEX-N-3D"></use></g><g data-mml-node="mn" transform="translate(2802.2,0)"><use data-c="31" xlink:href="#MJX-2266-TEX-N-31"></use></g><g data-mml-node="mtext" transform="translate(3302.2,0)"><use data-c="A0" xlink:href="#MJX-2266-TEX-N-A0"></use></g><g data-mml-node="mi" transform="translate(3552.2,0)"><use data-c="1D460" xlink:href="#MJX-2266-TEX-I-1D460"></use></g><g data-mml-node="mi" transform="translate(4021.2,0)"><use data-c="1D452" xlink:href="#MJX-2266-TEX-I-1D452"></use></g><g data-mml-node="mi" transform="translate(4487.2,0)"><use data-c="1D450" xlink:href="#MJX-2266-TEX-I-1D450"></use></g></g></g></svg></mjx-container> instabil.</p>


<p>\( \lim _{t \rightarrow \infty} x(t) \) existiert nicht.</p>


<p><mjx-container class="MathJax" jax="SVG"><svg alt=" \lim _{t \rightarrow \infty} x(t) " style="vertical-align: -0.566ex" xmlns="http://www.w3.org/2000/svg" width="11.356ex" height="2.262ex" role="img" focusable="false" viewBox="0 -750 5019.1 1000" xmlns:xlink="http://www.w3.org/1999/xlink"><defs><path id="MJX-2267-TEX-N-6C" d="M42 46H56Q95 46 103 60V68Q103 77 103 91T103 124T104 167T104 217T104 272T104 329Q104 366 104 407T104 482T104 542T103 586T103 603Q100 622 89 628T44 637H26V660Q26 683 28 683L38 684Q48 685 67 686T104 688Q121 689 141 690T171 693T182 694H185V379Q185 62 186 60Q190 52 198 49Q219 46 247 46H263V0H255L232 1Q209 2 183 2T145 3T107 3T57 1L34 0H26V46H42Z"></path><path id="MJX-2267-TEX-N-69" d="M69 609Q69 637 87 653T131 669Q154 667 171 652T188 609Q188 579 171 564T129 549Q104 549 87 564T69 609ZM247 0Q232 3 143 3Q132 3 106 3T56 1L34 0H26V46H42Q70 46 91 49Q100 53 102 60T104 102V205V293Q104 345 102 359T88 378Q74 385 41 385H30V408Q30 431 32 431L42 432Q52 433 70 434T106 436Q123 437 142 438T171 441T182 442H185V62Q190 52 197 50T232 46H255V0H247Z"></path><path id="MJX-2267-TEX-N-6D" d="M41 46H55Q94 46 102 60V68Q102 77 102 91T102 122T103 161T103 203Q103 234 103 269T102 328V351Q99 370 88 376T43 385H25V408Q25 431 27 431L37 432Q47 433 65 434T102 436Q119 437 138 438T167 441T178 442H181V402Q181 364 182 364T187 369T199 384T218 402T247 421T285 437Q305 442 336 442Q351 442 364 440T387 434T406 426T421 417T432 406T441 395T448 384T452 374T455 366L457 361L460 365Q463 369 466 373T475 384T488 397T503 410T523 422T546 432T572 439T603 442Q729 442 740 329Q741 322 741 190V104Q741 66 743 59T754 49Q775 46 803 46H819V0H811L788 1Q764 2 737 2T699 3Q596 3 587 0H579V46H595Q656 46 656 62Q657 64 657 200Q656 335 655 343Q649 371 635 385T611 402T585 404Q540 404 506 370Q479 343 472 315T464 232V168V108Q464 78 465 68T468 55T477 49Q498 46 526 46H542V0H534L510 1Q487 2 460 2T422 3Q319 3 310 0H302V46H318Q379 46 379 62Q380 64 380 200Q379 335 378 343Q372 371 358 385T334 402T308 404Q263 404 229 370Q202 343 195 315T187 232V168V108Q187 78 188 68T191 55T200 49Q221 46 249 46H265V0H257L234 1Q210 2 183 2T145 3Q42 3 33 0H25V46H41Z"></path><path id="MJX-2267-TEX-I-1D461" d="M26 385Q19 392 19 395Q19 399 22 411T27 425Q29 430 36 430T87 431H140L159 511Q162 522 166 540T173 566T179 586T187 603T197 615T211 624T229 626Q247 625 254 615T261 596Q261 589 252 549T232 470L222 433Q222 431 272 431H323Q330 424 330 420Q330 398 317 385H210L174 240Q135 80 135 68Q135 26 162 26Q197 26 230 60T283 144Q285 150 288 151T303 153H307Q322 153 322 145Q322 142 319 133Q314 117 301 95T267 48T216 6T155 -11Q125 -11 98 4T59 56Q57 64 57 83V101L92 241Q127 382 128 383Q128 385 77 385H26Z"></path><path id="MJX-2267-TEX-N-2192" d="M56 237T56 250T70 270H835Q719 357 692 493Q692 494 692 496T691 499Q691 511 708 511H711Q720 511 723 510T729 506T732 497T735 481T743 456Q765 389 816 336T935 261Q944 258 944 250Q944 244 939 241T915 231T877 212Q836 186 806 152T761 85T740 35T732 4Q730 -6 727 -8T711 -11Q691 -11 691 0Q691 7 696 25Q728 151 835 230H70Q56 237 56 250Z"></path><path id="MJX-2267-TEX-N-221E" d="M55 217Q55 305 111 373T254 442Q342 442 419 381Q457 350 493 303L507 284L514 294Q618 442 747 442Q833 442 888 374T944 214Q944 128 889 59T743 -11Q657 -11 580 50Q542 81 506 128L492 147L485 137Q381 -11 252 -11Q166 -11 111 57T55 217ZM907 217Q907 285 869 341T761 397Q740 397 720 392T682 378T648 359T619 335T594 310T574 285T559 263T548 246L543 238L574 198Q605 158 622 138T664 94T714 61T765 51Q827 51 867 100T907 217ZM92 214Q92 145 131 89T239 33Q357 33 456 193L425 233Q364 312 334 337Q285 380 233 380Q171 380 132 331T92 214Z"></path><path id="MJX-2267-TEX-I-1D465" d="M52 289Q59 331 106 386T222 442Q257 442 286 424T329 379Q371 442 430 442Q467 442 494 420T522 361Q522 332 508 314T481 292T458 288Q439 288 427 299T415 328Q415 374 465 391Q454 404 425 404Q412 404 406 402Q368 386 350 336Q290 115 290 78Q290 50 306 38T341 26Q378 26 414 59T463 140Q466 150 469 151T485 153H489Q504 153 504 145Q504 144 502 134Q486 77 440 33T333 -11Q263 -11 227 52Q186 -10 133 -10H127Q78 -10 57 16T35 71Q35 103 54 123T99 143Q142 143 142 101Q142 81 130 66T107 46T94 41L91 40Q91 39 97 36T113 29T132 26Q168 26 194 71Q203 87 217 139T245 247T261 313Q266 340 266 352Q266 380 251 392T217 404Q177 404 142 372T93 290Q91 281 88 280T72 278H58Q52 284 52 289Z"></path><path id="MJX-2267-TEX-N-28" d="M94 250Q94 319 104 381T127 488T164 576T202 643T244 695T277 729T302 750H315H319Q333 750 333 741Q333 738 316 720T275 667T226 581T184 443T167 250T184 58T225 -81T274 -167T316 -220T333 -241Q333 -250 318 -250H315H302L274 -226Q180 -141 137 -14T94 250Z"></path><path id="MJX-2267-TEX-N-29" d="M60 749L64 750Q69 750 74 750H86L114 726Q208 641 251 514T294 250Q294 182 284 119T261 12T224 -76T186 -143T145 -194T113 -227T90 -246Q87 -249 86 -250H74Q66 -250 63 -250T58 -247T55 -238Q56 -237 66 -225Q221 -64 221 250T66 725Q56 737 55 738Q55 746 60 749Z"></path></defs><g stroke="currentColor" fill="currentColor" stroke-width="0" transform="scale(1,-1)"><g data-mml-node="math"><g data-mml-node="munder"><g data-mml-node="mo"><use data-c="6C" xlink:href="#MJX-2267-TEX-N-6C"></use><use data-c="69" xlink:href="#MJX-2267-TEX-N-69" transform="translate(278,0)"></use><use data-c="6D" xlink:href="#MJX-2267-TEX-N-6D" transform="translate(556,0)"></use></g><g data-mml-node="TeXAtom" transform="translate(1422,-150) scale(0.707)" data-mjx-texclass="ORD"><g data-mml-node="mi"><use data-c="1D461" xlink:href="#MJX-2267-TEX-I-1D461"></use></g><g data-mml-node="mo" transform="translate(361,0)"><use data-c="2192" xlink:href="#MJX-2267-TEX-N-2192"></use></g><g data-mml-node="mi" transform="translate(1361,0)"><use data-c="221E" xlink:href="#MJX-2267-TEX-N-221E"></use></g></g></g><g data-mml-node="mi" transform="translate(3308.1,0)"><use data-c="1D465" xlink:href="#MJX-2267-TEX-I-1D465"></use></g><g data-mml-node="mo" transform="translate(3880.1,0)"><use data-c="28" xlink:href="#MJX-2267-TEX-N-28"></use></g><g data-mml-node="mi" transform="translate(4269.1,0)"><use data-c="1D461" xlink:href="#MJX-2267-TEX-I-1D461"></use></g><g data-mml-node="mo" transform="translate(4630.1,0)"><use data-c="29" xlink:href="#MJX-2267-TEX-N-29"></use></g></g></g></svg></mjx-container> existiert nicht.</p>


<p>\[<br />G_{0, K_{R}=1 \mathrm{sec}}=\frac{4 \mathrm{sec}^{-1}}{j \omega} \cdot \frac{1}{2 \mathrm{sec} \cdot j \omega+1} \cdot \frac{1}{0,5 \mathrm{sec} \cdot j \omega+1} <br />\]</p>


<p>\[<br />G_{S}(j \omega)=\frac{4 \sec ^{-2}}{(j \omega)^{2}+2 \sec \cdot(j \omega)^{3}} <br />\]</p>


<p>c) Intervall für <mjx-container class="MathJax" jax="SVG"><svg alt=" K_{R} " style="vertical-align: -0.373ex" xmlns="http://www.w3.org/2000/svg" width="3.323ex" height="1.918ex" role="img" focusable="false" viewBox="0 -683 1468.7 847.8" xmlns:xlink="http://www.w3.org/1999/xlink"><defs><path id="MJX-2272-TEX-I-1D43E" d="M285 628Q285 635 228 637Q205 637 198 638T191 647Q191 649 193 661Q199 681 203 682Q205 683 214 683H219Q260 681 355 681Q389 681 418 681T463 682T483 682Q500 682 500 674Q500 669 497 660Q496 658 496 654T495 648T493 644T490 641T486 639T479 638T470 637T456 637Q416 636 405 634T387 623L306 305Q307 305 490 449T678 597Q692 611 692 620Q692 635 667 637Q651 637 651 648Q651 650 654 662T659 677Q662 682 676 682Q680 682 711 681T791 680Q814 680 839 681T869 682Q889 682 889 672Q889 650 881 642Q878 637 862 637Q787 632 726 586Q710 576 656 534T556 455L509 418L518 396Q527 374 546 329T581 244Q656 67 661 61Q663 59 666 57Q680 47 717 46H738Q744 38 744 37T741 19Q737 6 731 0H720Q680 3 625 3Q503 3 488 0H478Q472 6 472 9T474 27Q478 40 480 43T491 46H494Q544 46 544 71Q544 75 517 141T485 216L427 354L359 301L291 248L268 155Q245 63 245 58Q245 51 253 49T303 46H334Q340 37 340 35Q340 19 333 5Q328 0 317 0Q314 0 280 1T180 2Q118 2 85 2T49 1Q31 1 31 11Q31 13 34 25Q38 41 42 43T65 46Q92 46 125 49Q139 52 144 61Q147 65 216 339T285 628Z"></path><path id="MJX-2272-TEX-I-1D445" d="M230 637Q203 637 198 638T193 649Q193 676 204 682Q206 683 378 683Q550 682 564 680Q620 672 658 652T712 606T733 563T739 529Q739 484 710 445T643 385T576 351T538 338L545 333Q612 295 612 223Q612 212 607 162T602 80V71Q602 53 603 43T614 25T640 16Q668 16 686 38T712 85Q717 99 720 102T735 105Q755 105 755 93Q755 75 731 36Q693 -21 641 -21H632Q571 -21 531 4T487 82Q487 109 502 166T517 239Q517 290 474 313Q459 320 449 321T378 323H309L277 193Q244 61 244 59Q244 55 245 54T252 50T269 48T302 46H333Q339 38 339 37T336 19Q332 6 326 0H311Q275 2 180 2Q146 2 117 2T71 2T50 1Q33 1 33 10Q33 12 36 24Q41 43 46 45Q50 46 61 46H67Q94 46 127 49Q141 52 146 61Q149 65 218 339T287 628Q287 635 230 637ZM630 554Q630 586 609 608T523 636Q521 636 500 636T462 637H440Q393 637 386 627Q385 624 352 494T319 361Q319 360 388 360Q466 361 492 367Q556 377 592 426Q608 449 619 486T630 554Z"></path></defs><g stroke="currentColor" fill="currentColor" stroke-width="0" transform="scale(1,-1)"><g data-mml-node="math"><g data-mml-node="msub"><g data-mml-node="mi"><use data-c="1D43E" xlink:href="#MJX-2272-TEX-I-1D43E"></use></g><g data-mml-node="TeXAtom" transform="translate(882,-150) scale(0.707)" data-mjx-texclass="ORD"><g data-mml-node="mi"><use data-c="1D445" xlink:href="#MJX-2272-TEX-I-1D445"></use></g></g></g></g></g></svg></mjx-container></p>


<p>\[<br />\begin{array}{llll}\alpha_{R}=60^{\circ} &amp; : &amp; \omega_{d 1}=0,22 \mathrm{sec}^{-1}, &amp; \left|G_{0}^{\prime}\left(j \omega_{d 1}\right)\right|=18,2 \mathrm{sec}^{-1} \\ \alpha_{R}=30^{\circ} &amp; : &amp; \omega_{d 2}=0,51 \mathrm{sec}^{-1}, &amp; \left|G_{0}^{\prime}\left(j \omega_{d 2}\right)\right|=7,7 \mathrm{sec}^{-1}\end{array} <br />\]</p>
<p><img style="width: 59%; height: auto; display: block; margin-left: auto; margin-right: auto;" src="https://storage.googleapis.com/max-academy-image-bucket/61bf8adfeb28c6349be78e9f.jpeg" alt="Abbildung" width="1227" height="1771" /></p>


<p>\[<br />\frac{1}{\left|G_{0}^{\prime}\left(j \omega_{d 1}\right)\right|} \leq K_{R} \leq \frac{1}{\left|G_{0}^{\prime}\left(j \omega_{d 2}\right)\right|} <br />\]</p>
<p>\[<br />\quad \ \, 0,055 \mathrm{sec} \leq K_{R} \leq 0,13 \mathrm{sec} <br />\]</p>

<p>Betrachtet wird der folgende Regelkreis</p>
<p><img style="width: 49%; height: auto; display: block; margin-left: auto; margin-right: auto;" src="https://storage.googleapis.com/max-academy-image-bucket/61bf88e3eb28c6349be789e0.jpeg" alt="Abbildung" width="338" height="90" /></p>
<p style="padding-left: 40px;">\[<br />\operatorname{mit} G_{R}(j \omega)=\frac{K_{R} \cdot j \omega}{0,5 \mathrm{sec} \cdot j \omega+1} <br />\]</p>
<p>Der Frequenzgang \( G_{0}(j \omega) \) des offenen Regelkreises ist für \( K_{R}=1 \) sec im Bodediagramm gegeben.</p>
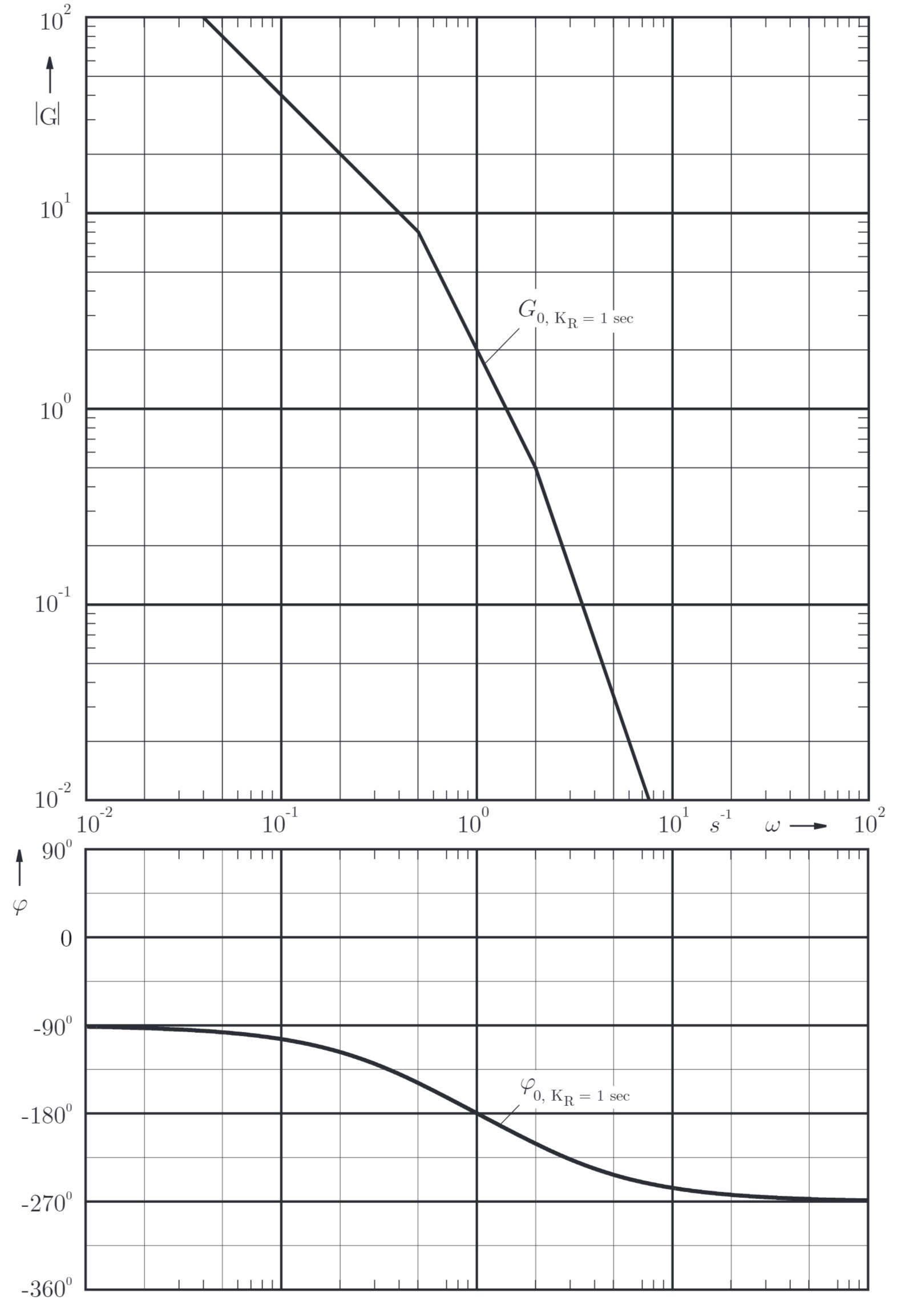
<p><img style="width: 69%; height: auto; display: block; margin-left: auto; margin-right: auto;" src="https://storage.googleapis.com/max-academy-image-bucket/61bf8a23eb28c6349be78d58.jpeg" alt="Abbildung" width="1124" height="1634" /></p>
<p> </p>
<ol style="list-style-type: lower-alpha;">
<li>Berechnen Sie für \( K_{R}=1 \) sec und einen Sprung der Führungsgröße<br />\[\quad w(t)= \begin{cases}0 &amp; , \quad t &lt; 0 \\ 1 &amp; , \quad t \geq 0\end{cases}\]<br />den stationären Endwert \( \lim _{t \rightarrow \infty} x(t) \), falls dieser existiert.</li>
<li>Geben Sie den Frequenzgang \( G_{S}(j \omega) \) der Regelstrecke in der folgenden Form an.<br />\[\quad G_{S}(j \omega)=K \cdot \frac{b_{0}+b_{1} \cdot j \omega+\ldots+b_{m} \cdot(j \omega)^{m}}{a_{0}+a_{1} \cdot j \omega+\ldots+a_{n} \cdot(j \omega)^{n}} \cdot e^{-T_{t} \cdot j \omega}\]</li>
<li>Bestimmen Sie das Intervall für \( K_{R} \) so, dass für die Phasenreserve \( \alpha_{R} \) des Regelkreises \( 30^{\circ} \leq \alpha_{R} \leq 60^{\circ} \) gilt.</li>
</ol>
<p><strong>Hinweis:</strong> Alle Aufgabenteile sind unabhängig voneinander lösbar. Für den Betragsverlauf genügt die Betrachtung der Asymptoten.</p>

Dies ist eine interaktive Aufgabe zu: Sprungfunktion mit praktischen Tipps zum Lösen und einer Zusammenfassung der nötigen Theorie

Aufgabenstellung:

Lösungsweg:

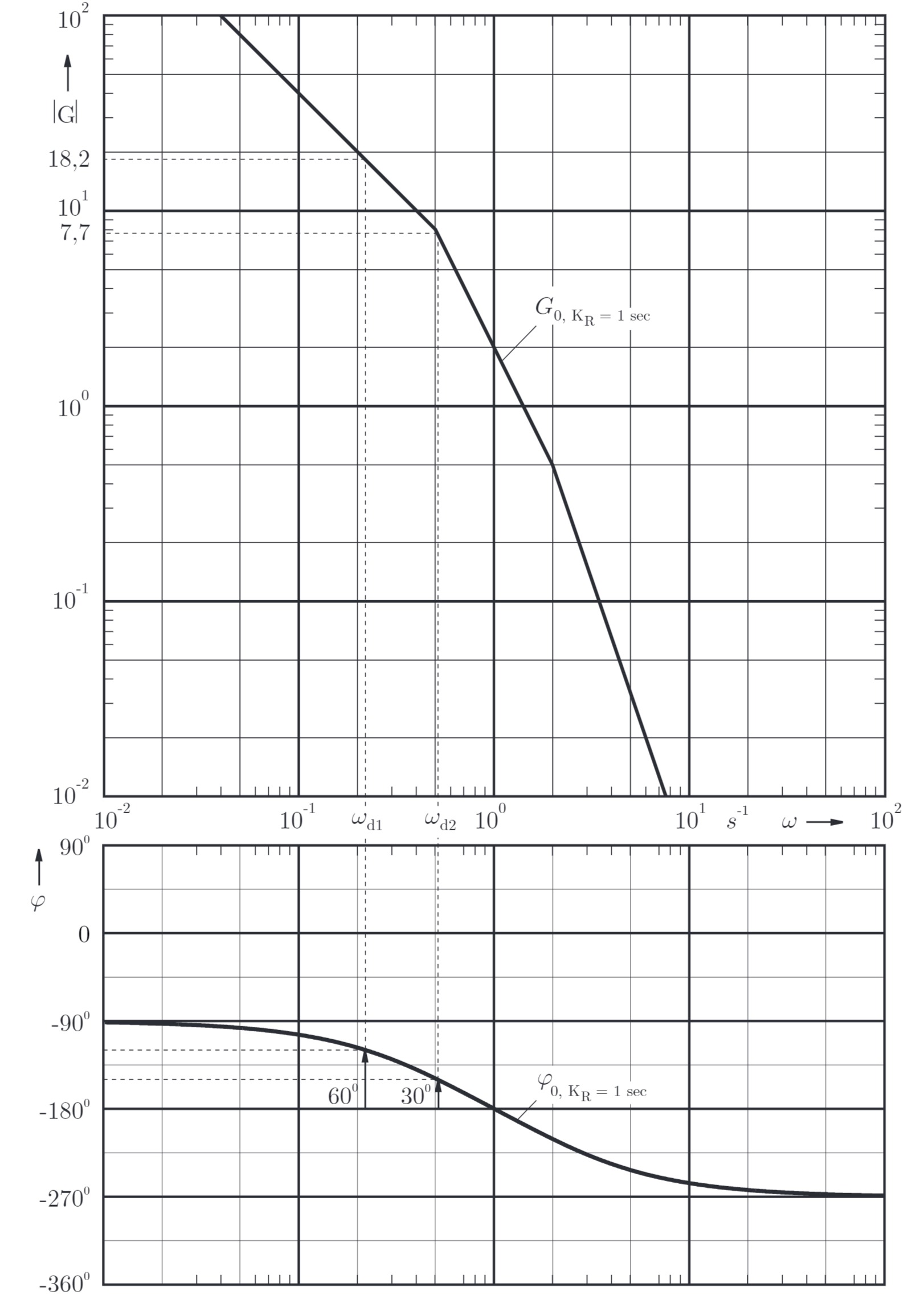
Lösung: