2 / 4

Aufgabenstellung:

Gegeben ist ein Ausschnitt des Zeitverlaufs eines periodischen Signals , das eine Überlagerung zweier harmonischer Schwingungen mit den Kreisfrequenzen und darstellt:

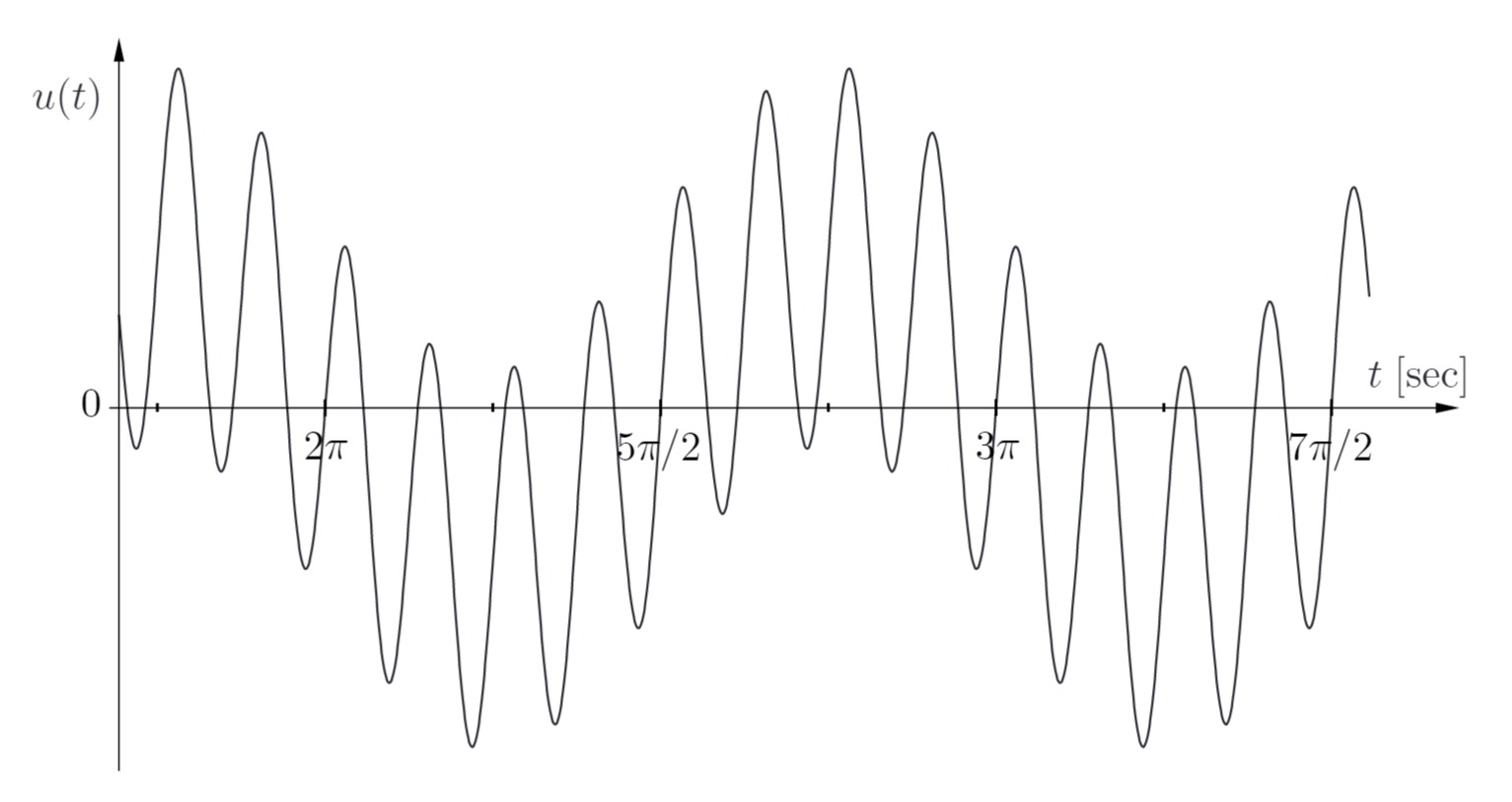
Abbildung

a) Bestimmen Sie die Kreisfrequenzen und .

Zur Verwendung in einem zeitdiskreten Regelkreis soll das gegebene Signal diskretisiert werden. Das Signal wird mit abgetastet.


b) Ist die Wahl von sinnvoll? Begründen Sie.
Mit welcher minimalen Kreisfrequenz muss das gegebene Signal abgetastet werden, um eine fehlerfreie Rekonstruktion zu gewährleisten?


Um Aliasing-Effekte während der Abtastung des vorliegenden Signalverlaufs zu verhindern, soll ein Anti-Aliasing Filter verwendet werden. Für das Filter werden folgende Vorgaben getroffen:

  • Es soll ein Tiefpassfilter erster Ordnung verwendet werden.
  • Signalanteile der maximal auftretenden Frequenz in sollen um abgeschwächt werden.
  • Niederfrequente Signalanteile sollen nahezu unverändert durchgelassen werden.

c) Berechnen Sie ein Anti-Aliasing Filter, das die gegebenen Vorgaben erfüllt. Geben Sie das Filter in der Form an.

d) Berechnen Sie die durch die Filterung entstehende Phasenverschiebung bei den im Signal auftretenden Kreisfrequenzen und

Lösungsweg:

Drücke auf "Aufdecken" um dir den ersten Schritt der Lösung anzuzeigen

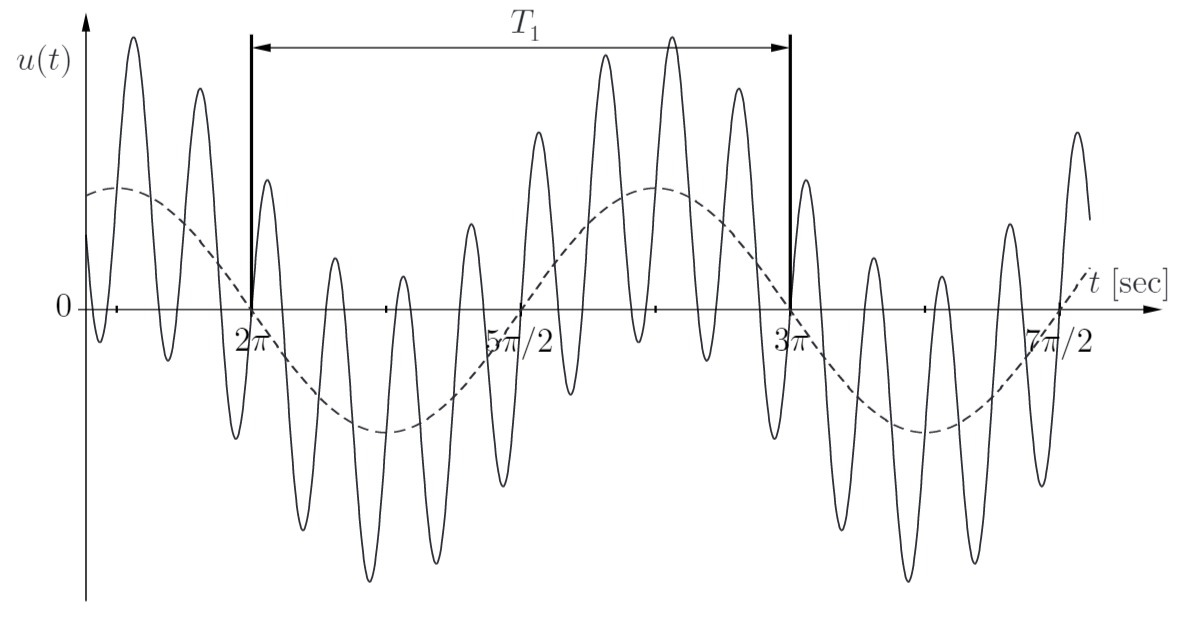
Abbildung

a) und

Ablesen von und :

Innerhalb der eingezeichneten Periodendauer (s. Diagramm) liegen 8 vollständige Schwingungen der höheren Frequenz vor. Es gilt daher:

b) Wahl von sinnvoll? minimale Kreisfrequenz

Die gewählte Abtastfrequenz ist nicht sinnvoll, da das ShannonTheorem nicht eingehalten wurde .

Die höchste Frequenz ist . Folglich muss die minimale Abtastfrequenz betragen.

c)  

Ansatz:

Niederfrequente Signalanteile sollen nahezu unverändert durchgelassen werden

Signalanteile der maximal auftretenden Frequenz sollen um abgeschwächt werden

d) Phasenverschiebung

und bzw. einsetzen

Lösung:

  2.   ist nicht sinnvoll,