Aufgabenstellung:
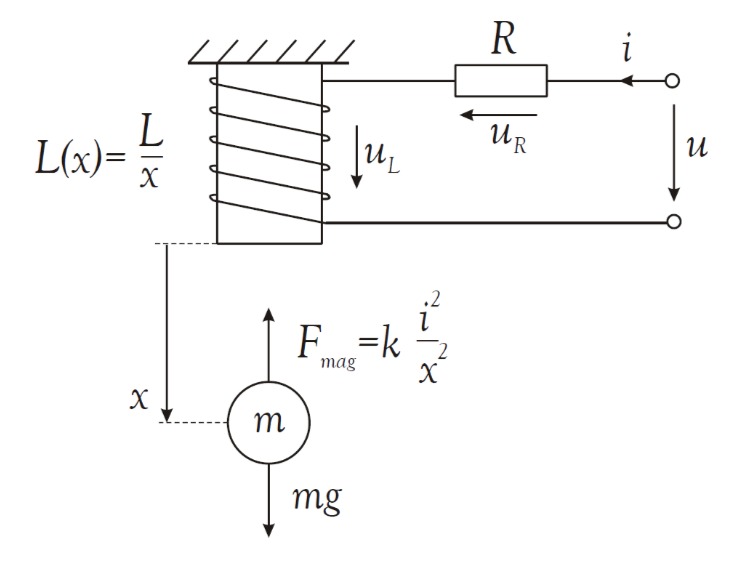
Gegeben ist das dargestellte System eines elektrischen Hubmagnetes.
Für das System wurden folgende Differentialgleichungen aufgestellt:
Des Weiteren existiert die Ruhelage des System bei
-
Linearisieren Sie das dargestellte System um die angegebene Ruhelage bei einer konstanten Eingangsspannung
. -
Stellen Sie das linearisierte System in Form eines Blockschaltbildes dar.
Lösungsweg:
a) Linearisierung um die angegebene Ruhelage
Beide Differentialgleichungen enthalten nichtlineare Terme, die mehrere zeitabhängige Größen enthalten, daher ist eine mehrdimensionale Taylor-Reihenentwicklung notwendig.
Diese ergibt sich zu
Ersetzt man in (2) die zeitabhängigen Größen durch die Beschreibung der Ruhelagen-Abweichung ergibt sich
Elektrisches Teilsystem:
In Gleichung (3) muss folgender Teil linearisiert werden
Diese Gleichung wird nun durch den mehrdimensionalen Taylor-Ansatz linear approximiert. Hierzu gilt es zunächst die drei partiellen Ableitungen nach den drei zeitabhängigen Größen aus der ursprünglichen DGL zu bilden
In
Einsetzen in
Für
Somit ergibt sich die linearisierte DGL des elektrischen Teilsystems
Das Einsetzen der Ruhelagen liefert schlussendlich
Mechanischen Teilsystems:
Analoger Ansatz wird bei der DGL (4) angewendet. Hier muss der folgende Teil linearisiert werden.
Hierzu werden ebenfalls zunächst die beiden partiellen Ableitungen des nichtlinearen Gliedes der ursprünglichen Differentialgleichung gebildet, um die Differenzenfunktion zu approximieren
Aufstellen der zweidimensionalen Taylor-Näherung des Terms ergibt
Der Term wird nun in (4) eingesetzt. wodurch sich ergibt
Durch anschließendes Einsetzen der Ruhelage
Schlussendlich ergibt sich durch das Einsetzen von
b) Blockschaltbild
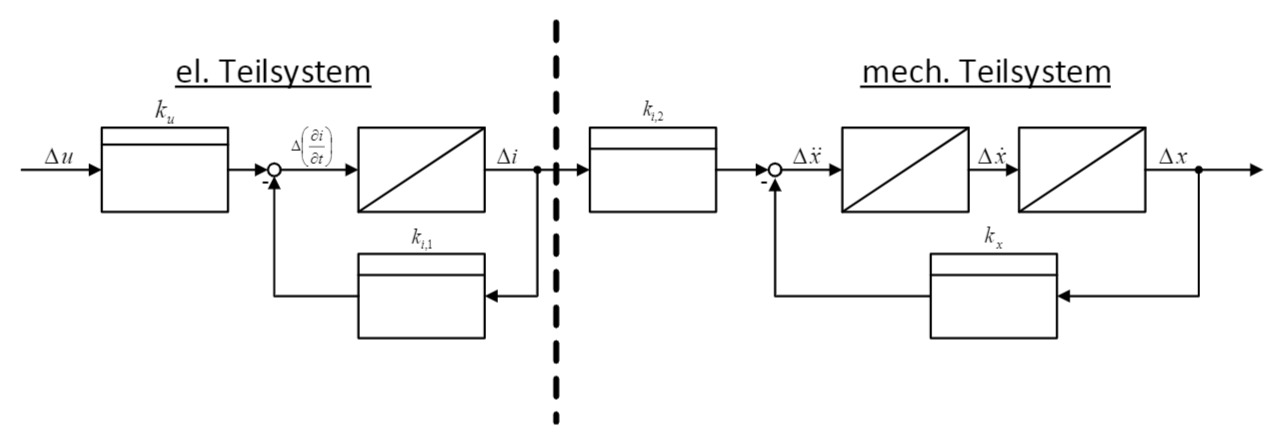
Lösung:
Siehe Musterlösung.