Aufgabenstellung:
Gegeben ist die Strecke
a) Skizzieren Sie das Bodediagramm von
b) Berechnen Sie anschließend die Parameter eines Reglers
so, dass der geschlossene Regelkreis folgende Anforderungen erfüllt:
Dabei soll für die Zeitkonstante
Lösungsweg:
a) Bodediagramm von

b) Parameter von
Die Knickfrequenzen für das Bodediagramm sind
Die Anforderungen an den geschlossenen Regelkreis lauten
Daraus ergeben sich die Kenngrößen
Zunächst wird die Ist-Phase in
Die Phase muss also in
Hierfür wird ein PD-Regler verwendet
Für die Phase des Reglers bei
Bemerkung: Falls
Der Verstärkungsfaktor
Abschließend muss
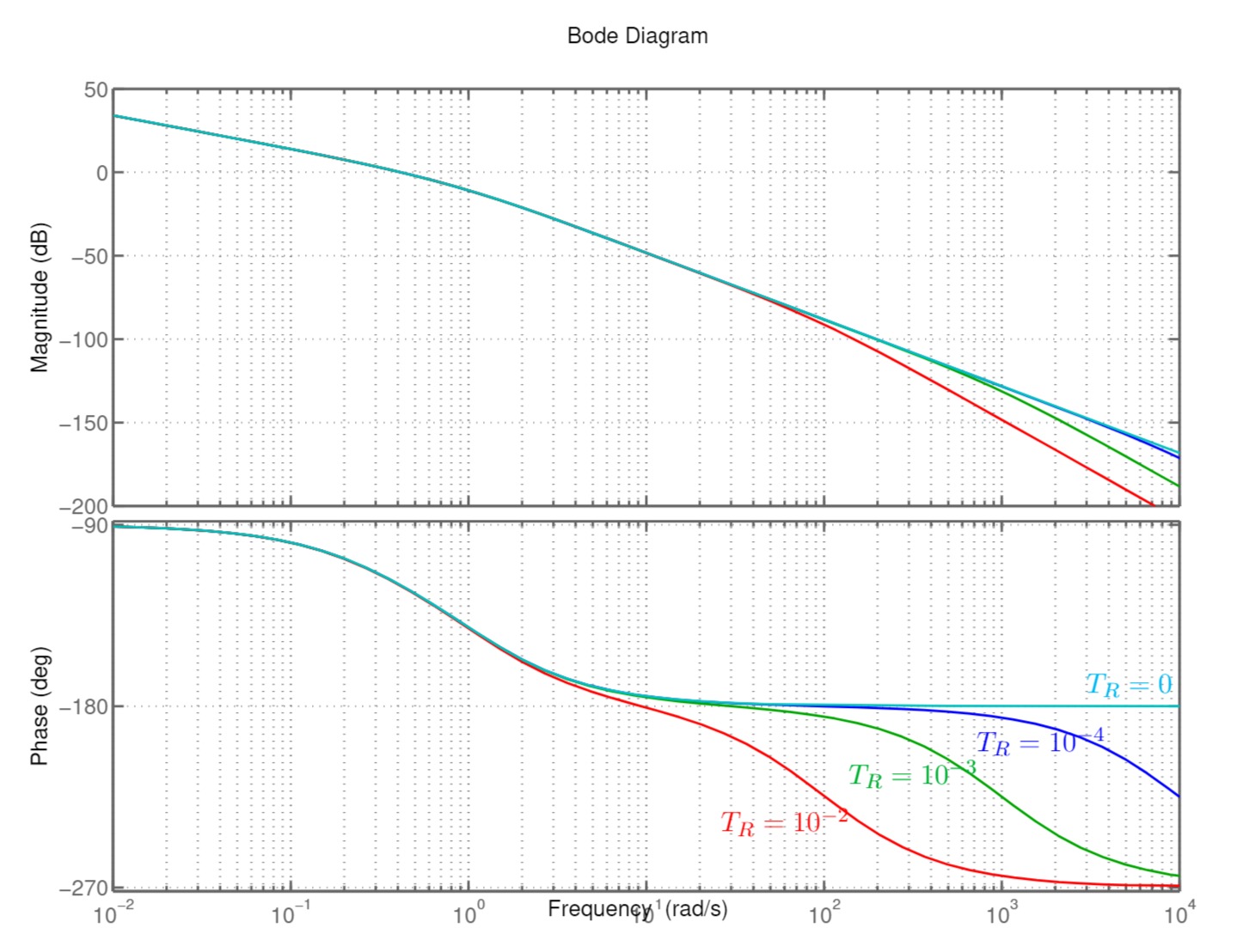
Es wird hier
Lösung:
Es wird ein PD-Regler verwendet
mit