Aufgabenstellung:
Betrachtet wird das folgende System:
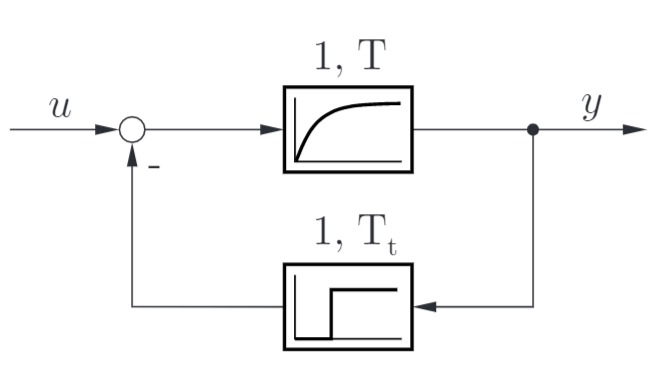
a) Ist das System für alle
Hinweis: Die folgenden Aufgabenteile können unabhängig gelöst werden.
Das System soll jetzt diskretisiert werden. Es gilt nun
b) Bestimmen Sie die Differenzengleichung für das System in der Form
mit der Abtastzeit
c) Es gilt nun:
Lösungsweg:
a) Stabilität für
Anwendbarkeit des vereinfachten Nyquist-Kriterium prüfen
Betrag fällt monoton, da der Betrag des
b) Differenzengleichung bestimmen
Ubertragungsfunktion des geschlossenen Regelkreises aufstellen:
Laplace Rücktransformation in den Zeitbereich:
Diskretisieren mit Hilfe der Rückwärtsdifferenz:
c)
Ansatz:
Mit
Lösung:
- stabil