Aufgabenstellung:
Gegeben ist ein System, von dem folgender Frequenzgang
Das System soll wie nachstehend abgebildet geregelt werden, wobei keine bleibend Regelabweichung auftreten soll. Zunächst gilt
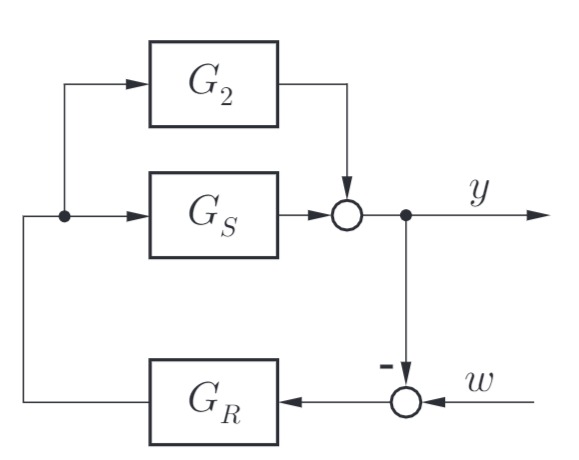
a) Prüfen Sie für einen
Aus Kostengründen soll nun ein einfacher
b) Berechnen Sie für
c) Bestimmen Sie die maximale Reglerverstärkung
Hinweis: Der folgende Aufgabenteil d) ist unabhängig von den bisherigen Aufgabenteilen a)-c) lösbar.
Nun gilt für das parallel geschaltete System
d) Ermitteln Sie mithilfe des Hurwitz-Kriteriums, für welche Werte
Lösungsweg:
a) Anforderungen prüfen
Die Strecke besitzt bereits integrierendes Verhalten, daher ist auch bei Verwendung eines
b) Durchtrittsfrequenzen
Wie aus der Übertragungsfunktion ersichtlich ist, handelt es sich um einen Integrator mit
Ortskurve (Skizze):
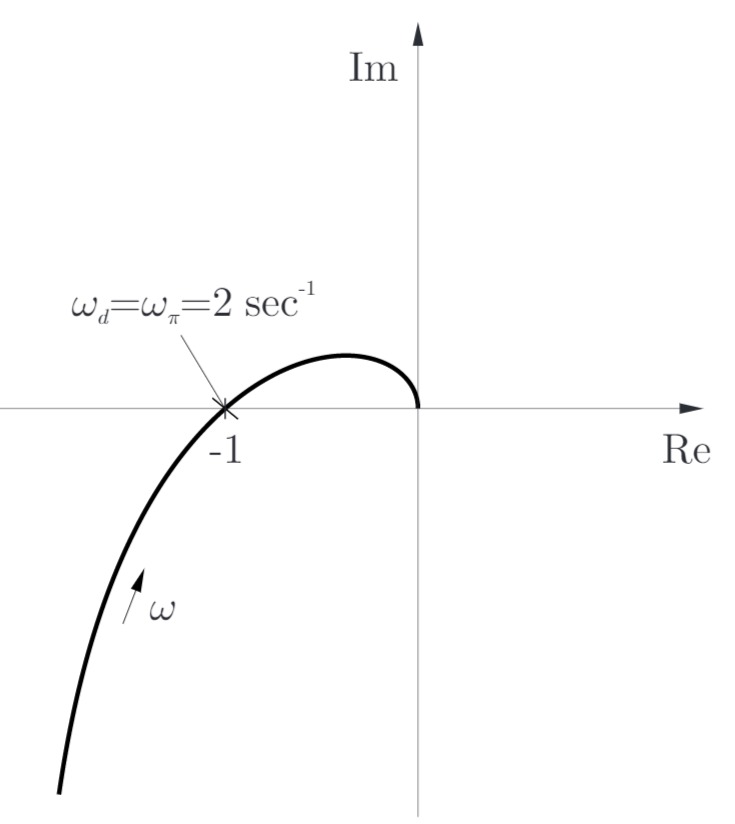
c) Maximale Reglerverstärkun, sowie die Phasenreserve
Da
Maximales
Damit folgt
Analog zu b) ergibt sich die veränderte Durchtrittsfrequenz zu
Mit
ergibt sich für
Hinweis: Das vereinfachte Nyquist-Kriterium ist anwendbar.
d) Hurwitz-Kriteriums
Die Übertragungsfunktion der Parallelschaltung aus
Die Übertragungsfunktion des geschlossenen Regelkreises ergibt sich zu
Das entsprechende Nennerpolynom lautet
1. Bedingung nach Hurwitz:
2. Bedingung nach Hurwitz:
Durch Reduktion auf die restriktivsten Bedingungen ergibt sich
Lösung:
- siehe Musterlösung