13 / 15

Aufgabenstellung:

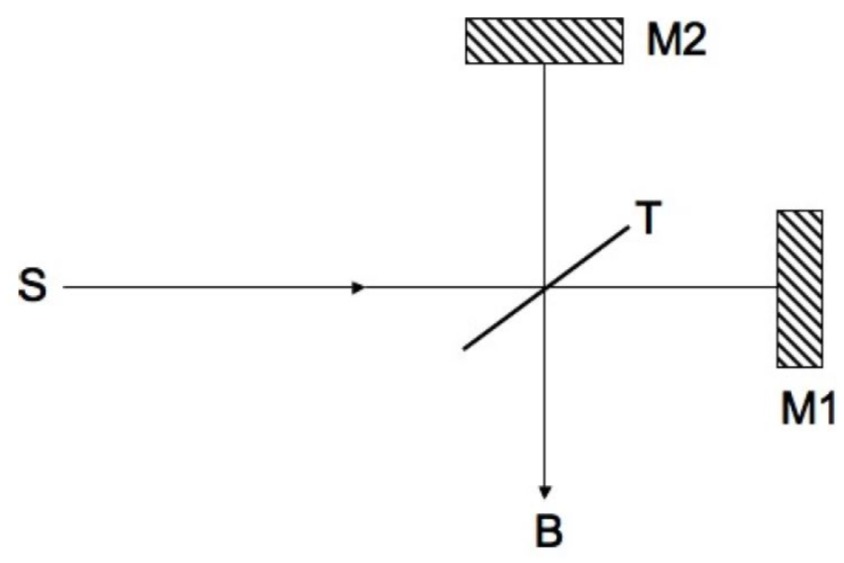
Abbildung

  1. Die Quelle emittiere zunächst monochromatische Strahlung der Wellenlänge . Im Punkt beobachtet man das Auftreten von Interferenzmaxima, wenn der Spiegel M1 um die Strecke in Strahlrichtung verschoben wird. Bestimmen sie die Wellenlänge
  2. Zwischen Strahlteiler und Spiegel wird nun eine evakuierte Zelle der länge gestellt. Während des Auffüllens der Zelle mit -Gas bis zum Atmosphärendruck wird das Auftreten von Interferenzmaxima beobachtet. Bestimmen Sie den Brechungsindex von bei Atmosphärendruck. Wie lang muss dazu die Köheränzzeit des Lasers sein?

  3. Mit dem Michelson-Interferometer können zwei eng benachbarte Wellenlängen aufgelöst werden. In Abhängigkeit von der Verschiebung des Spiegels beobachtet man maximale Intensität, wenn die einzelnen Interferenzbilder für die Strahlung der beiden Wellenlängen zusammenfallen. Die Quelle emittiere nun zwei Strahlungen der Wellenlangen und mit . Die Strecke, die der Spiegel zwischen zwei benachbarten maximaler Intensität verschoben werden muss, ist . Bestimmen Sie .

  4. Wieviele Spalte muss ein Gitterspektrograph mindestens besitzen, wenn dieselben Wellenlängen und in erster Ordnung aufgelöst werden sollen.

Lösungsweg:

Drücke auf "Aufdecken" um dir den ersten Schritt der Lösung anzuzeigen

a) Wellenlänge

Die zusätzliche Weglänge, die der Strahl nach der Verschiebung durchlaufen hat, ist:

Damit ergibt sich eine Wellenlänge von .

b) Brechungsindex und Koheränzzeit

Nun wird der Spiegel nicht mehr verschoben. Anfangs ist eine evakuierte Zelle im Strahlweg, die einen optischen Weg von darstellt. Füllt man die Zelle mit , so ändert sich der Brechungsindex in der Zelle und somit der optische Weg.

Nach Aufgabenstellung werden Maxima durchlaufen, weswegen der zusätzliche Wegunterschied wie folgt ist:

Daraus folgt der Brechungindex:

Die Kohärenzzeit lässt sich aus der Kohärenzlänge berechnen, diese muss mindestens dem Gangunterschied entsprechen.

c) Gangunterschied

Verschieben wir nun wieder den Spiegel. Anfangs schieben wir den Spiegel so in Position, dass wir eine konstruktive Interferenz erreichen (sowohl als auch interferieren konstruktiv). Nun verschieben wir den Spiegel um d und erhalten erst wieder ein Maximum, wenn sowohl die Wellenlänge , als auch wieder ein Maximum am Schirm haben.

Mit gilt:

Daraus folg also:

d) Anzahl Spalten für gleiche Auflösung

Die Auflösung eines Gitters mit Strichen ist gegeben durch:

Für die 1.Ordnung folgt .

Lösung: