Aufgabenstellung:
Kurvengleichung in Polarkoordinaten:
- Bestimmen Sie den Definitionsbereich (Winkelbereich) und skizzieren Sie den Kurvenverlauf mit Hilfe einer Wertetabelle (Schrittweite:
. - Wie lautet die Kurvengleichung in kartesischen Koordinaten in impliziter Form?
Lösungsweg:
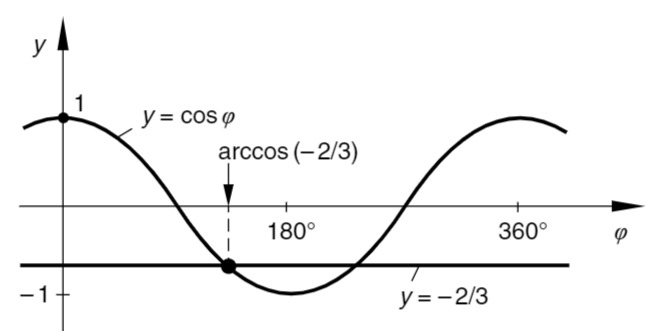
a) Definitionsbereich
Wegen der Spiegelsymmetrie der Kurve bezüglich der
Zum Definitionsbereich gehören alle Winkel zwischen
Definitionsbereich:
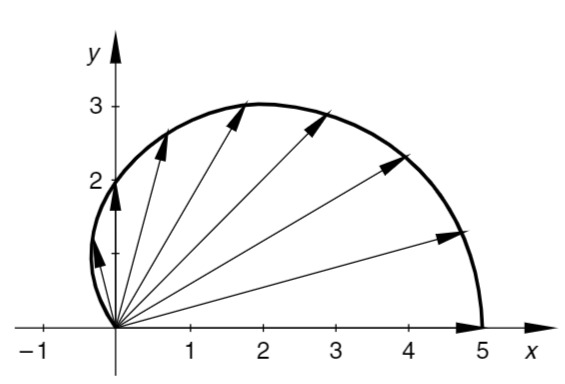
Skizze
Kurvenverlauf: Die Skizze zeigt den Kurvenverlauf im Winkelbereich
Wertetabelle für den 1 . und 2. Quadranten:
Skizze
b) Wir benötigen die Transformationsgleichungen