Aufgabenstellung:
Die Bewegung eines Körpers, der von der Erdoberfläche aus mit der Geschwindigkeit
mit
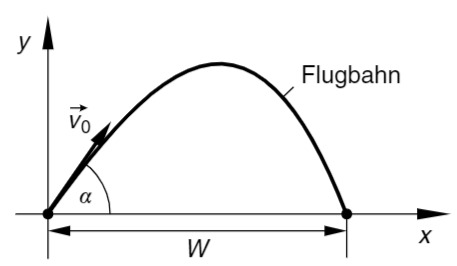
- Wie lautet die Bahnkurve in explizieter Form?
- Berechnen Sie Flugzeit
und Wurfweite . - Welche Ergebnisse erhält man im luftleeren Raum (dort gilt
)? Welche maximale Höhe erreicht der Körper (Wurfhöhe )?
Lösungsweg:
a) Explizieter Form
Wir lösen die 1 . Gleichung nach
Hinweis: Es wurden beide Seiten mit
Genutzte Umformungen:
b) Berechnung der Flugzeit
Die Parametergleichung
Aus der Bedingung
Hinweis: Der 2.Summand wurde zunächst mit
Die untere Gleichung liefert die Flugzeit
Hinweis: Beide Seiten wurden mit
Berechnung der Wurfweite
Die Wurfweite
Genutzte rechenregel:
c) Sonderfall luftleerer Raum
Die Bahnkurve lautet:
Die Flugbahn ist eine Parabel (auch „Wurfparabel" genannt, Skizze).
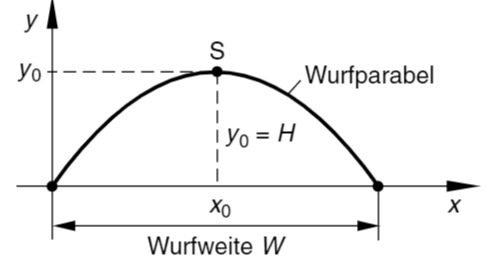
Flugzeit
Hinweis: Es wurde die trigonometrische Beziehung
Wurfhöhe
Die Wurfhöhe
Hinweis: Es wurde die trigonometrische Beziehung