Aufgabenstellung:
Berücksichtigt man beim freien Fall den Luftwiderstand durch eine dem Quadrat der Fallgeschwindigkeit
- Welcher Zusammenhang besteht zwischen der Fallgeschwindigkeit
und dem Fallweg ? - Welche Endgeschwindigkeit
wird erreicht? - Welche Strecke muss der Körper fallen, um die halbe Endgeschwindigkeit zu erreichen?
Wie lange ist er dann bereits unterwegs?
Lösungsweg:
a) Zusammenhang zwischen Fallgeschwindigkeit
Mit Hilfe der Formeln
Setze vorübergehend
Damit erhalten wir für
Nun lösen wir das Weg-Zeit-Gesetz, durch Entlogarithmierung nach
Diesen Ausdruck setzen wir in das Geschwindigkeit-Zeit-Gesetz ein und erhalten die gesuchte Abhängigkeit der Fallgeschwindigkeit
Verwendete Rechenregeln:
b) Endgeschwindigkeit (nach unendlich langer Fallzeit und damit auch unendlich langem Fallweg):
Umformungen: Der Grenzübergang
Damit können wir den Zusammenhang zwischen
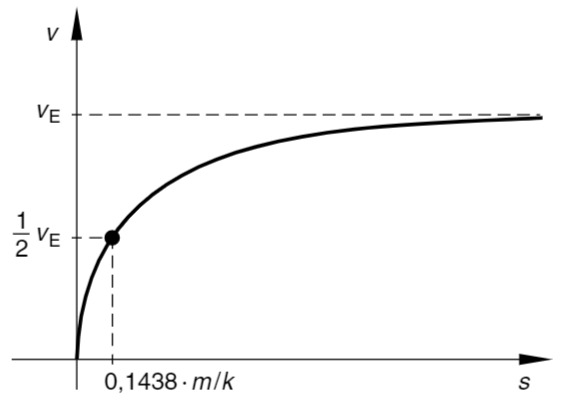
c) Fallweg und Zeit bis zum erreichen der halben Endgeschwingigkeit
Stelle
Nutze:
Umformen nach
Stelle
Auflösen dieser Gleichung durch Übergang zur Umkehrfunktion Areatangens hyperbolicus: