Aufgabenstellung:
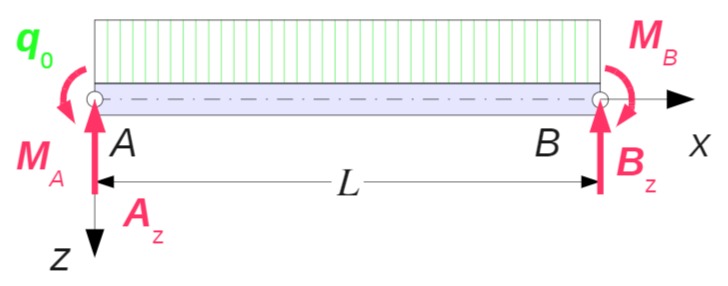
Der abgebildete Balken mit der Biegesteifigkeit
Gesucht sind die Lagerreaktionen, der Verlauf der Schnittlasten, die Biegelinie
sowie der Wert des größten Biegemoments

Zahlenwerte:
Lösungsweg:
Die Aufgabe kann durch viermalige Integration der Streckenlast gelöst werden:
Randbedingungen:
Auflösen der Randbedingungen am rechten Ende nach
Damit gilt für die Schnittlasten:
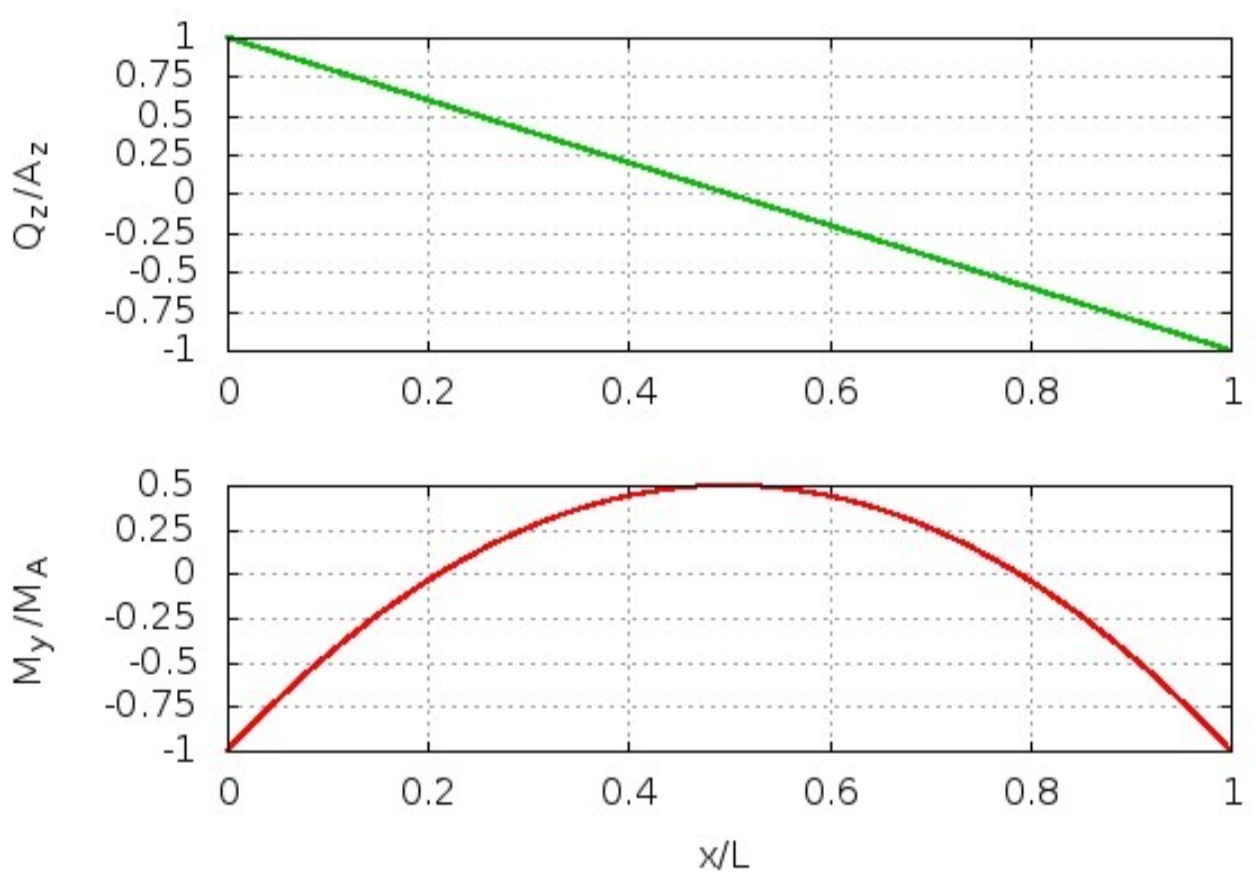
Die Lagerreaktionen können aus den Schnittlasten bestimmt werden:
Das größte Biegemoment tritt an der Stelle auf, an der die Querkraft null ist:
Dieser Wert ist vom Betrag kleiner als die Einspannmomente. Das betragsmäßig größte Biegemoment tritt daher an den Einspannstellen auf:
Für die Biegelinie folgt:
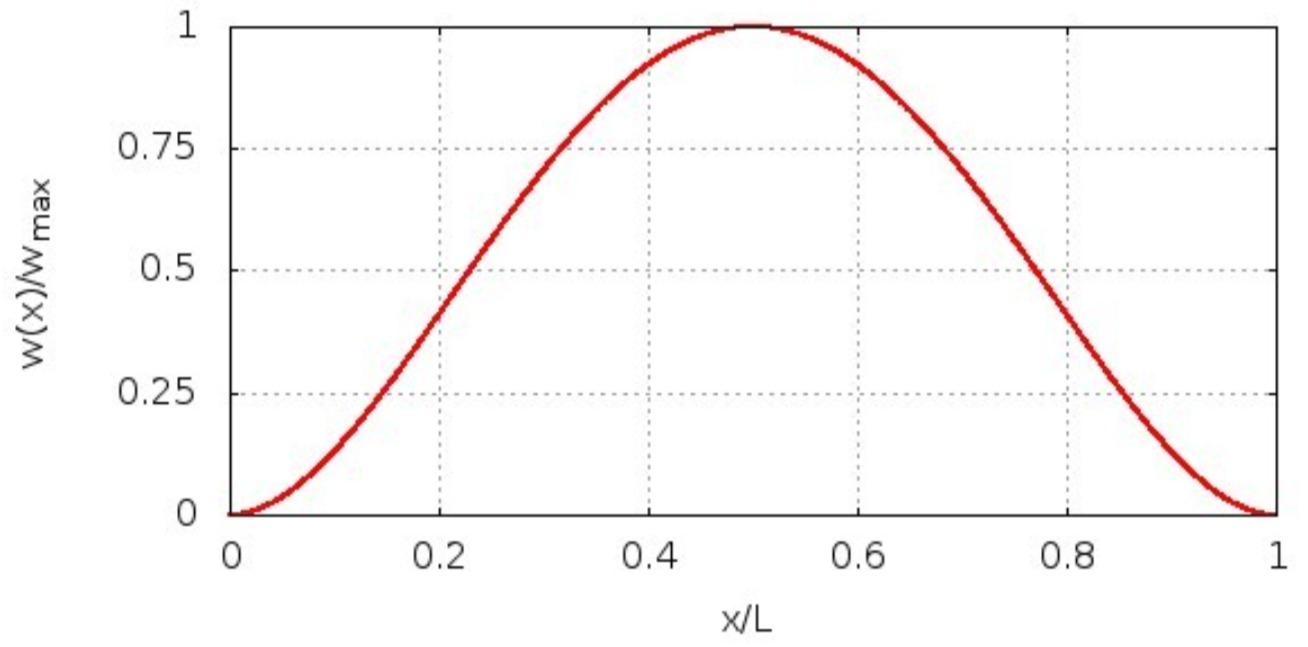
Die größte Durchbiegung tritt an der Stelle auf, an der der Biegewinkel null ist:
Der Biegewinkel ist am linken und rechten Ende und in der Mitte null. Die größte Durchbiegung tritt in der Mitte auf:
Zahlenwerte:
